Class B Push Pull Amplifier - Engineering Projects

In class B push pull amplifier, output current (collector current) flows for only half the cycle of the input signal. Hence distortion is excessive. Single ended operation is, therefore, not possible in class B audio amplifier. Class B audio (un-tuned) amplifier must necessarily use push pull operation to reduce distortion. In effect, in class B push pull amplifier, one transistor say Q₁ conduct during one half cycle while the other transistor namely Q₂ conducts during the other half cycle.

Class A power amplifiers may use either single ended or push pull operations. However, in most class A power amplifier, push pull operation is preferred because of the various merits mentioned above.

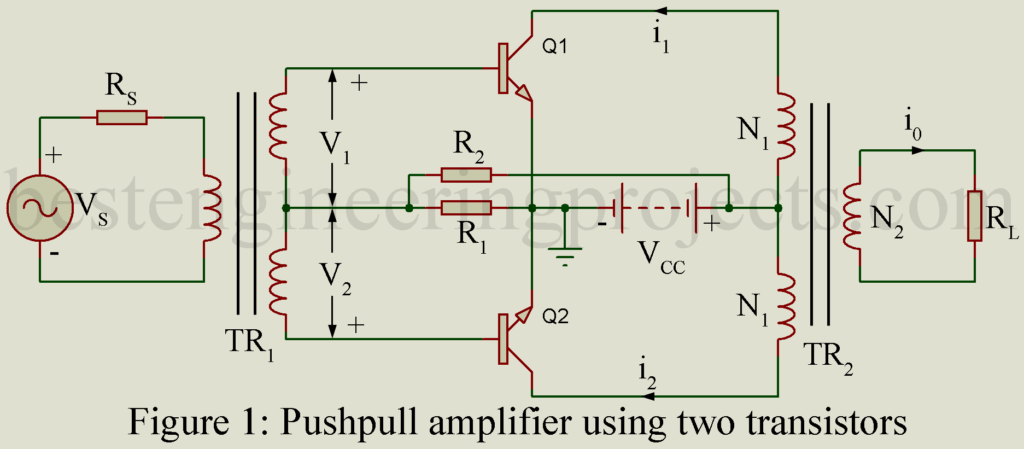
The circuit of class B push pull amplifier is the same as that of class A push pull amplifier. The difference lies in the order of biasing. In class B circuit, the transistor are biased approximately to cutoff. Hence the circuit of figure 1 represents class B push pull amplifier also if resistor R₁ is made zero because a silicon transistor is basically at cutoff if its base is short circuited to emitter.

Advantage of Class B Push pull Amplifier over class A Push pull Amplifier

Greater power output
Higher conversion efficiency
Negligible power loss with zero signal

Because of zero power drainage with zero signal, in amplifiers using solar cell or simple batteries, class B operation is preferred.

Drawbacks of class B Pushpull Amplifier

Harmonic distortion is higher
Self-biased not be used
Supply voltage is required to have good regulation

Collector Circuit Efficiency | Class B Push Pull Amplifier

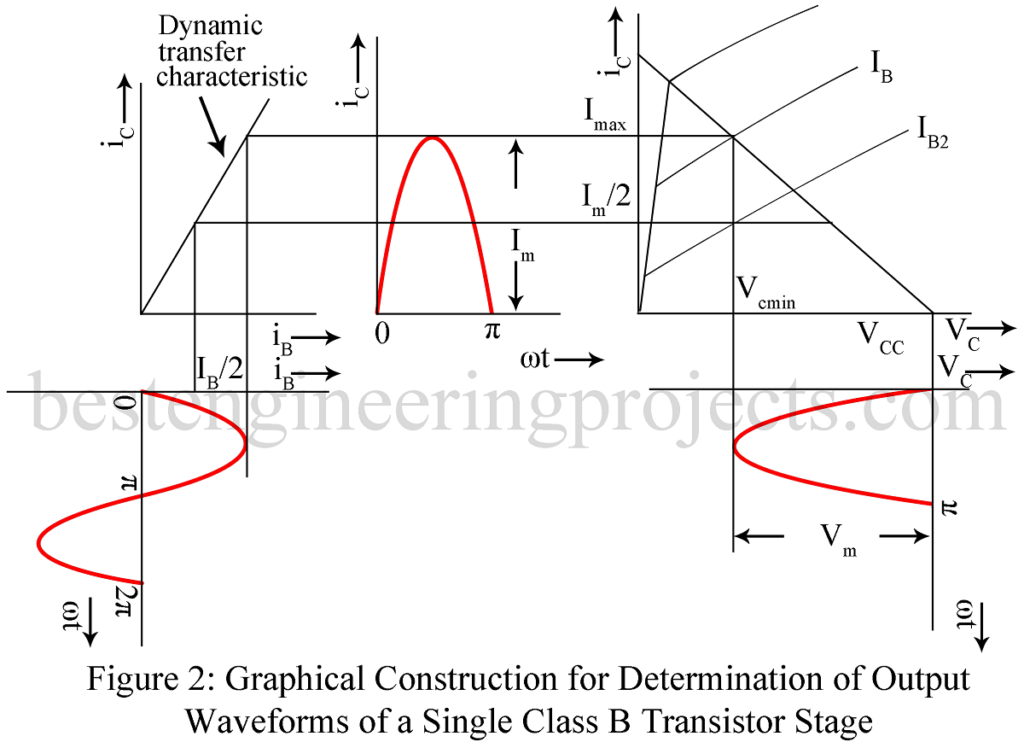
We assume that the transistor characteristics are linear, parallel and equi-spaced for equal increments of excitation so that the dynamic transfer characteristics is a straight line as shown in figure 2. We also assume that the minimum current is zero. Figure 2 demonstrates the graphical method of determination of collector current and collector voltage wave shaped for a single transistor say transistor Q₁ operating under class B condition.

With sinusoidal excitation base current i_B, the collector current i_C and the collector voltage v_C are also sinusoidal during one-half of the a.c. cycle and zero during the other half. The effective load resistance R_L1 for one transistor is $R_{L1} = (\dfrac{N_1}{N_2})^2 \times R_L$ where R_L is the load resistance across the secondary of the output transformer TR₂, N₁ is the number of turns on one-half of the primary and N₂ is the number of turns on the secondary as shown in figure 1.

Waveform of i_c and v_c corresponding to transistor Q₁ alone. Waveform of transistor Q₂ are similar to those shown in figure 2 but 180⁰ out of phase. Hence the load current in the secondary being proportional to the difference of the two collector currents, forms a perfect sine wave.

Power output $P_o = \dfrac{I_m\times V_m}{2} = \dfrac{I_m}{2}[V_{CC}-V_{min}]$ …….(1)

D.C. load line in each transistor under loaded condition is the average value of the half sine wave of i_c of figure 2. Hence for this half sine wave,

$I_{dc} = \dfrac{I_m}{\pi}$ ……(2)

Hence the dc power input to both the transistors form the collector supply is,

$P_i = \dfrac{2I_m \times V_{CC}}{\pi}$ …….(3)

Hence collector circuit efficiency is,

$\eta = \dfrac{P_0}{P_i} \times 100 % = \dfrac{\pi}{4} \times \dfrac{V_m}{V_{CC}} \times 100%$ …..(4)

$= \dfrac{\pi}{4}(1-\dfrac{V_{min}}{V_{CC}})\times 100%$ ……(5)

Equation 5 shows that the maximum possible value of collector circuit efficiency for class B amplifier is $25\pi$ i.e. 78.5%. This maximum theoretical value is higher than the corresponding value of 50% for class A transformer coupled amplifier.

For such transistor circuit where V_min << V_CC, collector circuit efficiency closely approaches the theoretical maximum limit. Basically, this high value of collector circuit efficiency in class B amplifier becomes possible because of the fact that in class B amplifier, current is zero with zero excitation whereas in class A amplifier, there is drain from V_CC source even at zero signal. It is worth nothing that in a class B amplifier, collector dissipation is zero signal and increases with increase of signal magnitude while in a class A amplifier, collector dissipation is maximum with zero signal and decreases with increases of signal magnitude.

In class B amplifier, the d.c. component of collector current increase with increase of signal. Hence power supply regulation must be good.

Collector Dissipation of Class B Push Pull Amplifier

Total collector dissipation P_D in both transistors is equal to the dc power input from collector supply voltage minus the power delivered to the load. Hence,

$P_D = P_i-P_o = \dfrac{2I_mV_{CC}}{\pi}-\dfrac{I_mV_m}{2}$ ……(6)

But $I_m = \dfrac{V_m}{R_{L1}}$ …….(7)

Hence $P_D = \dfrac{2}{\pi}\times \dfrac{V_{CC}V_{m}}{R_{L1}}-\dfrac{V_m^2}{2R_{L1}}$ ……..(8)

With zero excitation, V_m = 0. Hence, as per equation 8, collector dissipation is zero with zero excitation. Using equation 8, it may be shown that the collector dissipation increases with increase of excitation and passes through a maximum at $V_m = \dfrac{2V_{CC}}{\pi}$ .

Hence maximum collector dissipation P_D, max is obtained from Equation 8 on putting $V_m = \dfrac{2V_{CC}}{\pi}$ . ……(9)

Thus, $P_{Dmax} = \dfrac{2}{\pi} \times \dfrac{V_{CC}}{R_{L1}}\times \dfrac{2V_{CC}}{\pi}-\dfrac{1}{2R_{L1}}(2\dfrac{V_{CC}}{\pi})^2 = \dfrac{2V_{CC}^2}{\pi^2R_{L1}}$ ……..(10)

Maximum Power Output of Class B Push Pull Amplifier

Maximum output power is obtained when V_m = V_CC i.e. when V_min = 0. Hence,

$P_{omax} = \dfrac{I_m V_{CC}}{2} = \dfrac{V_{CC}^2}{2R_L}$ …….(11)

From equation (10) and (11) we find that,

$P_{Dmax} = \dfrac{4}{\pi^2} \times P_{omax} = 0.4 P_{omax}$ ……(12)

From equation (12) we conclude that the two transistors of a class B amplifier taken together must be able to dissipate about 40% of the maximum power output. For a class AB amplifier designed to deliver maximum power output of say 50 watts, P_Dmax – 20 watts i.e. each transistor must be capable of dissipating 10 watts. Hence, we conclude that class B pushpull amplifier is capable of providing output power 5 times the power dissipation capability of each transistor.

On the other hand, in class A amplifier using parallel operation of two transistor to get the same output power of 50 watts, assuming maximum conversion efficiency of 50%, dc power requirement is $P_i = \dfrac{P_o}{\eta} = \dfrac{50}{0.5} = 100$ watts. This complete power of 100 watts must be dissipated in the two transistors are zero signal. Thus, each transistor must be capable of dissipating 50 watts. Thus, with zero excitation, in class A operation there is a steady loss of 50 watts in each transistor whereas in class B amplifier the standby or zero excitation collector dissipation is zero. This clearly establishes the superiority of class B push pull operation over class A parallel operation.

Distortion in Class B Push Pull Amplifier

In a push pull amplifier, even harmonic get eliminated from the output. Then the only harmonic distortion of significance is the hard-harmonic distortion. Thus, is given by,

$D_3 = \dfrac{|B_3|}{|B_1|}$ …….(13)

Power output, taken distortion into account, is given by,

$P = (1 + D_3^2) \times \dfrac{B_1^2 R_{L1}}{2}$ …….(14)

Example 1 The idealized pushpull class B power amplifier shown in figure 1 has R₂ = 0, V_CC = 24 volts, N₂ = 2N₁ and R_L = 10 -ohm. The transistors have hfe = 30. Input is sinusoidal. For the maximum output signal at V_m = V_CC, determine (a) the output signal power (b) the collector dissipation in each transistor. Also calculator the maximum collector dissipation per transistor.

Solution: $R_{L1} = (\dfrac{N_1}{N_2})^2 \times R_L = (\dfrac{1}{2})^2 \times 10 = 2.5-ohm$

When V_m= V_CC, power output is

$P_{max} = \dfrac{V_{CC}^2}{2R_L} = \dfrac{(24)^2}{2 \times 2.5} = 115.2 watts$

Total collector dissipation in the two transistors is,

$P_D = \dfrac{2}{\pi}\times \dfrac{V_{CC}\times V_m}{R_{L1}}-\dfrac{V_m^2}{2R_{L1}}$

At $V_m = V_{CC}$ ,

$P_D = \dfrac{2}{\pi}\times \dfrac{V_{CC}^2}{R_{L1}}-\dfrac{V_{CC}^2}{2R_{L1}}$

$= \dfrac{V_{CC}^2}{R_{L1}}(\dfrac{2}{\pi}-\dfrac{1}{2})$

$= \dfrac{24^2}{2.5}(0.6366-0.5) = 31.47 watts$

Hence dissipated in each transistor = $\dfrac{31.47}{2} = 15.73 watts$

$P_{Dmax} = \dfrac{2V_{CC}^2}{\pi^2R_{L1}} = \dfrac{1\times 24^2}{\pi^2 \times 2.5^2} = 46.688 watts$

Hence maximum collector dissipation per transistor $= \dfrac{46.688}{2} = 23.344 watts$

2 Thoughts to “Class B Push Pull Amplifier”

Feel the rthm

September 8, 2021 at 5:51 pm

Can u help me with this

Anidealclass Bpushpullpoweramplifierwithinput andoutput transformers have Vcc=20V, N2=2N1and RL=20Ω. The transistors have hfe=20. L et input be sinusoidal.
Forthe maximumoutput signalat VCE(p)=Vcc. Determine i) the output signalpower ii)thecollectordissipationineachtransistoriii)theconversionefficiency.

Krishna

May 9, 2022 at 9:55 am

Wonderful explanation