Cascading of Amplifier Stages - Engineering Projects

What is Cascading of Amplifier Stages?

A single stage of amplifier can provide only a limited current gain or voltage gain. Most of the applications require much higher gain. Hence, we usually use several amplifier stages connected in cascade i.e. connected such that the output of one stage becomes the input to the next stage. Thus, a multistage amplifier or cascade amplifier may provide a higher voltage gain or current gain.

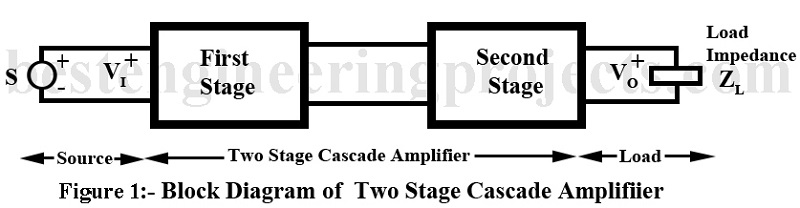
Cascading of amplifier stages is usually done to increase the total gain of the amplifier. However, sometimes cascading is done to get the desired output and input impedance for specific applications. Figure 1 gives the block diagram of two-stage amplifier. The first stage is driven by a voltage source V_s having series source resistance R_s. Alternatively, the driving source may be current source I_s with shunt resistance R_s. the output of the first stage is fed to the input of the second stage while the output of the second stage feeds the load impedance Z_L.

Actual voltage available at the input of the first stage is V_i while V₀ is the output voltage of the second stage. Then the ratio $\dfrac{V_o}{V_i}$ forms the voltage gain of the two stage cascade amplifier. Instead of two stages as shown in figure 3, we may have three or more stages connected in cascade amplifier, it becomes possible to amplify a weak input voltage V_i of just a few microvolts to get an output voltage V₀ of several volts.

Cascading of Amplifier Stage using Transistor

Transistor amplifier may be connected in any of the three configurations namely common emitter (CE), common base (CB) and common collector (CC). However, in cascade amplifier meant for providing high gain, only CE amplifier stage are connected in cascade. CB and CC configurations can not be used for this purpose.

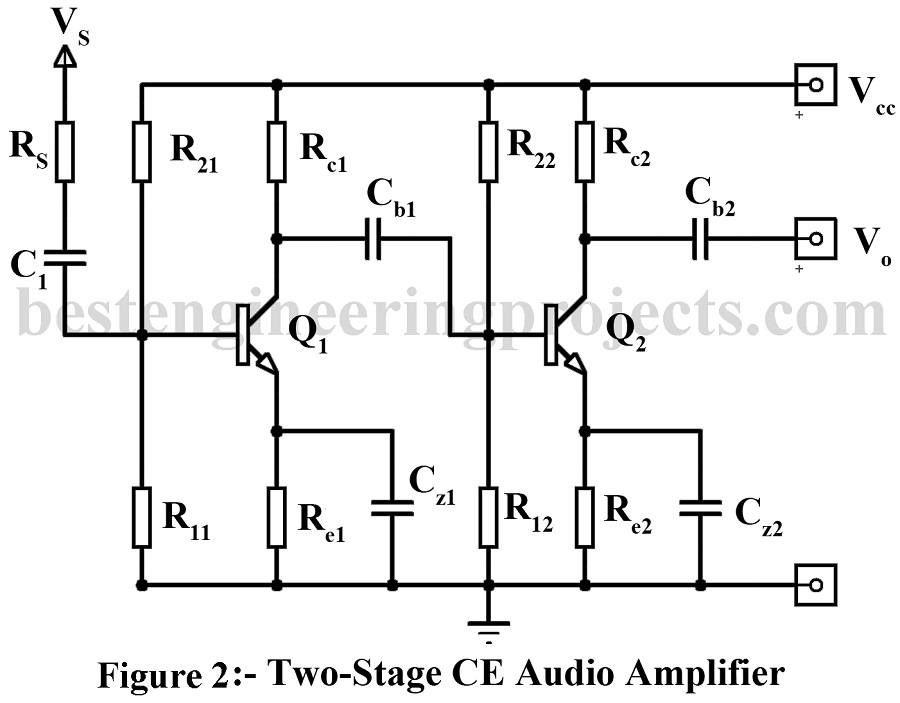
Figure 2 gives the circuit of a two stage CE audio amplifier. The circuit gives the typical biasing arrangement and use of coupling capacitors C_b1 and C_b2. Typical values of circuit components are also given. The load impedance is a resistor while coupling is through a capacitor. Hence this cascade amplifier forms the so-called resistance – Capacitance coupled or RC coupled amplifier. Other circuit arrangement is also popular for specific uses. However, we here take up R.C. coupled amplifier since this is the one most popularly used for audio frequency amplification. Circuit of figure 2 is given here just to give an impression as to what a typical 2-stage CE audio amplifier looks like.

Analysis | Cascading of Amplifier Stages

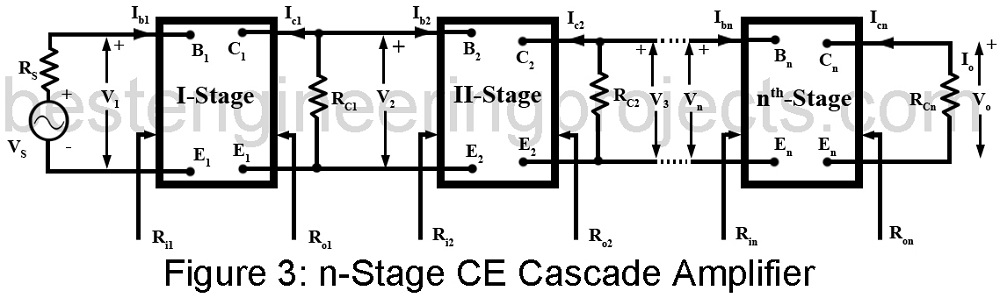
For the purpose of analysis we take up a general n-stage CE cascade amplifier. Figure 3 gives the block diagram of the same giving the various voltages, currents and resistances involved. In Figure 3, the biasing arrangement and coupling elements have not been shown for the sake of celerity. We now proceed to derive expressions for voltage gain, current gain, power gain, input impedance and output impedance of this amplifier.

(A) Voltage Gain:

The voltage gain of the complete cascade amplifier is simply the product of the voltage gains of the individual stage. This is proved below.

Voltage gain of first stage is,

$A_{V1} = \dfrac{V_2}{V_1} = \dfrac{Output\ voltage\ of\ the\ first\ stage}{ Input\ voltage\ of\ the\ first\ stage }$

$= A_{V1}<\theta_1$ …..(1)

Where A_V1 is the magnitude of the voltage gain and $\theta_1$ is the phase angle of the output voltage V₂ relative to the input voltage V₁. The output voltage V₂ of the first stage forms the input voltage of the second stage. Hence

Voltage gain of second stage is,

$A_{V2} = \dfrac{V_3}{V_2} = \dfrac{ Output\ voltage\ of\ the\ second\ stage }{ Input\ voltage\ of\ the\ first\ stage}$

$= A_{V2} <\theta_2$ ……(2)

Similar expressions may be written for the remaining stages.

Then the voltage gain of the complete n-stage cascade amplifier is given by,

$A_V = \dfrac{V_0}{V_1} = \dfrac{ Output\ voltage\ of\ the\ n^{th}\ stage }{ Input\ voltage\ of\ the\ first\ stage }$

$= A_V<\theta$ …..(3)

Where A_v is the magnitude of the voltage gain and $\theta$ is the phase angle of the output voltage V₀ relative to the input voltage V₁

But $\dfrac{V_0}{V_1}=\dfrac{V_2}{V_1}\times \dfrac{V_3}{V_2}\times {V_4}{V_3}\ . \ . \ . \ . \dfrac{V_n}{V_{n-1}}\times \dfrac{V_0}{V_n}$ ……(4)

From equation 4 we conclude that

$A_V = A_{V1}\times A_{V2}\times A_{V3}\ .\ . \ . \ . A_{Vn-1}\times A_{Vn}$ ……(5)

Or $A_V <\theta = A_{V1}\times A_{V2}\times A_{V3}\ .\ . \ . \ . A_{Vn-1}\times A_{Vn}$

$= <\theta_1 + \theta_2 +\ .\ . \ . \ . +\theta_n$ …..(6)

Hence $A_V = A_{V1}\times A_{V2}\times A_{V3}\ .\ . \ . \ . A_{V2}$ ……(7)

And $\theta = \theta_1 + \theta_2 + \theta_3 +\ .\ . \ . \ . + \theta_n$ ……(8)

From Equation (7) we conclude that the magnitude of voltage gain of the complete cascade amplifier is equal to the product of the magnitude of voltage gains of the individual stages.

From Equations 8 we conclude that the phase shift of the voltage gain of the complete cascade amplifier is equal to the sum of the phase shift of the individual stages.

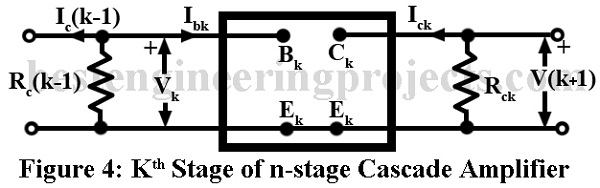
Calculation of the Voltage Gain A_vk of K^th stage:

Figure 4 shows one intermediate stage, say k^th stage, of n-stage cascade amplifier.

Then the voltage gain of this k^th stage is given by,

$A_{vk} = \dfrac{A_{IK}\times R_{LK}}{R_{ik}}$ …..(9)

Where R_ik is the effective load impedance at the collector of the k^thstage.

Quantities A_IK, R_LK and R_ik may be evaluated on starting from the last stage i.e. n^th stage and processing backward. Thus, for the n^th stage, current gain A_Ln and input resistance R_in are given by,

$A_{In} = \dfrac{-h_{fe}}{1+h_{oe}\times R_{Ln}}$ ……..(10)

And,

$R_{in} = h_{ie} + h_{re}\times A_{In} \times R_{Ln}$ ….(11)

Where R_Ln is the effective load impedance of the last stage and is equal to R_en.

For the (n-1)^th stage, effective load impedance R_i(n-1) is equal to R_c(n-1) || R_in. Thus,

$R_{i(n-1)} = \dfrac{R_{c(n-1)}\times R_{in}}{R_{c(n-1)} + R_{in}}$ …..(12)

Next we calculate the current gain A_I(n-1) of the (n-1)^th stage using Equation 10 on replacing R_Ln by R_L(n-1). Similarly, we calculate the input impedance R_i(n-1) of the (n-1)^th stage from Equation 9 no replacing A_In by A_I(n-1) and R_Ln by R_L(n-1). Thus, we procced backward to calculate the current gain and input impedance of each stage from n^th to the first. Then the voltage gain of each stage may be calculated using Equation 8 relevant to the stage.

Voltage gain of the complete cascade amplifier may then be calculated using Equation 5.

Calculation of Current Gain A_I of K^th Stage

$A_I = \dfrac{I_0}{I_{b1}} = -\dfrac{I_{cn}}{I_{b1}}$ …..(13)

Now $-\dfrac{I_{cn}}{I_{b1}} = -\dfrac{I_{c1}}{I_{b1}}\times \dfrac{I_{c2}}{I_{c1}}\times \dfrac{I_{cc}}{I_{c2}}\times \ .\ . \ . \ . \dfrac{I_{cn}}{I_{c(n-1)}}$ ……(14)

Or, $A_I = \grave{A}_{I1} \times \grave{A}_{I2} \times \grave{A}_{I3} \times \ .\ . \ . \ . \ \grave{A}{In}$ …..(15)

Where A_I1 is the base-to-collector current gain of the first stage and equals $-\dfrac{I_{c1}}{I_{b1}}$ while A’_I2, A’_I3 etc. are the collector-to-collector current gains of second, third etc. stages.

For k^th stage, collector-to-collector current gain A’_IK is given by

$\grave{A}_{IK} = \dfrac{I_{ck}}{I_{c(k-1)}}$ …..(16)

Similarly, base-to-collector current gain A_IK is given by

$A_{IK} = -\dfrac{I_{ck}}{I_{bk}}$ …..(17)

Relation between A’_IK and A_IK

From Figure 4,

$I_{bk} = -I_{c(k-1)}\times \dfrac{R_{c(k-1)}}{R_{c(k-1)} + R_{ik}}$ …..(18)

Where R_ik is the input impedance of the k^th stage.

Hence $\grave{A}_{IK} = \dfrac{I_{ck}}{I_{c(k-1)}} = \dfrac{I_{ck}}{I_{bk}}\times \dfrac{I_{bk}}{I_{c(k-1)}} = A_{IK}\times \dfrac{R_{c(k-1)}}{R_{c(k-1)} + R_{ik}}$ …..(19)

Value of A’_IK as given by Equation 19 may be substituted in equation 15 to give the resultant current gain A_I.

Steps involved in Evaluating Current gain A_I

Find the base-to-collector current gain A_In for the n^th or the last stage making use of equation 10.
Find the input impedance of the last stage making use of Equations 11.
Calculate the effective load resistance R_L(n-1) for the (n-1)^th stage using Equation 12
Repeat steps 1 to 3 for (n-1)^th, (n-1)^th stage to find the A_IK for the k^th stage.
Find the collector-to-collector gain A’_IK for the k^th stage using equation 19.
Find the resultant current gain A_Ifor the complete n-stage cascade amplifier using Equation 15.

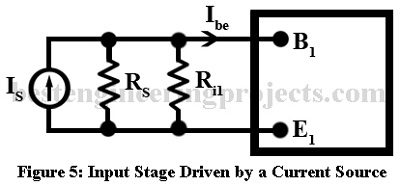
Overall Current Gain Considering the source Resistance:

Let the input stage of the n-stage cascade amplifier be driven from a current source I_s as shown figure 5. Then the overall current gain of the cascade amplifier is given by,

$A_{IS}=\dfrac{R_s}{R_s + R_{i1}}$ …..(20)

Alternative Method of Calculating A_I | Cascading of Amplifier Stages

Alternative we may calculate A_I making use of the following relation:

$A_v = A_I \times \dfrac{R_{cn}}{R_{i1}}$ …….(21)

Where A_v is the voltage gain of the complete cascade amplifier.

$A_P = \dfrac{Output\ power\ of\ the\ last\ stage}{ Input\ power\ of\ the\ first\ stage } = -\dfrac{V_0 \times I_{cn}}{V_1 \times I_{b1}} = A_V \times A_I$ …..(22)

Alternative using Equation 21, we get, $A_P = (A_I)^2\times \dfrac{R_{en}}{R_{i1}}$ …..(23)

Input Impedance | Cascading of Amplifier Stages

The input impedance of the complete cascade amplifier may be found following the same procedure as for calculating the voltage gain. Thus, we start from the last stage and proceed backward. The steps involved are as below:

Calculate base-to-collector current gain A_In for the last stage using Equation 10.
Calculate input impedance R_in of the last stage using Equation 11.
Calculate effective load impedance $R_{L(n-1)}$ for the (n-1)^th stage using Equations 12.
Calculate $A_{I(n-1)}$ and $R_{L(n-1)}$ for the (n-1)^th stage and $R_{L(n-2)}$ for the (n-2)^th
Proceed in this manner and finally calculate the input impedance of the first stage.

Output Impedance | Cascading of Amplifier Stages

For calculating the output impedance of each stage and that of the complete cascade amplifier, we proceed forward starting from the first stage. The output admittance of the first stage is given by,

$Y_{01} = h_{oe}-\dfrac{h_{fe}\times h_{re}}{h_{ie} + R_{s}}$ …..(24)

Then $\dfrac{1}{Y_{01}}$ gives the corresponding output impedance R₀₁.

The output terminal impedance R_ot1 of the first stage is equal to the parallel combination of R₀₁and R_oc1.

Thus $R_{ot1} = \dfrac{R_{01}\times R_{c1}}{R_{01} + R_{c1}}$ …..(25)

This R_ot1 forms the source impedance for the second stage. Equation 24 may now be used again to find Y₀₂ of the second stage using R_0t1 in place of R_s. The output terminal impedance R_ot2 of the second stage is parallel combination of $R_{02}(==\dfrac{1}{Y_{02}})$ and R_C2.

We may proceed in this manner to find the output impedance of the third, fourth etc. stage and finally the last stage. In the above derivation we have assumed CE configuration. However, the method given above for calculating A_V, A_I, R_i and R₀ is general in nature and may also be used for CB and CC configurations.

Choice of Transistor Configuration in a Multistage Amplifier

Choice of transistor configuration to be used for intermediate stages in a multistage amplifier depends on the maximum voltage gain provided by the configuration. hence CC configuration can not be used since a stage of CC amplifier gives voltage gain less than unity. A single stage CB amplifier, no doubt, gives voltage gain more than unity but intermediate stage can not use even CB configuration since the overall voltage gain of multistage amplifier using VB configuration is low, almost equal to the voltage gain of the last stage alone. This becomes evident from the following discussion.

The voltage gain A_Vk of any stage, say K^th stage is given by,

$A_{Vk} = \dfrac{A_{IK}\times R_{Lk}}{R_{ik}}$ ……(26)

But, $R_{Lk} = R_{ck}|\ | R_{i(k+1)}$ …..(27)

Hence, $R_{Lk} < R_{i(k+1)}$

Assuming the stage to be identical i.e. assuming that R_i(k+1) = R_ik, we conclude that R_LK < R_ik. Further the maximum value of current gain A_IK in CB configuration in h_fb which is slightly less than unity. Hence as per Equation 26, A_Vk for any CB stage except the last stage is less than unity. Hence we conclude that even CB configuration is not suitable for use in intermediate stages.

CE stage are popularly used for intermediate stages since h_fe for a CE stage is much greater than unity.

Input Stage | Cascading of Amplifier Stages

For input stage, the consideration is not the maximum voltage gain but the impedance matching of the source with the input impedance of the input stage. Some driving sources may require input circuit to be an almost open circuit while others need an almost short circuit. Hence we may be required to use CC or CB configuration for the input stage for proper impedance match at the cost of voltage or current gain. In certain other cases, choice of configuration for the input stage is the minimization of noise and maximization of single/noise power ratio.

What is Cascading of Amplifier Stages?

Cascading of Amplifier Stage using Transistor

Analysis | Cascading of Amplifier Stages

(A) Voltage Gain:

Calculation of the Voltage Gain Avk of Kth stage:

Calculation of Current Gain AI of Kth Stage

Relation between A’IK and AIK

Steps involved in Evaluating Current gain AI