Resistance Capacitance Coupled or R.C. Coupled Amplifier

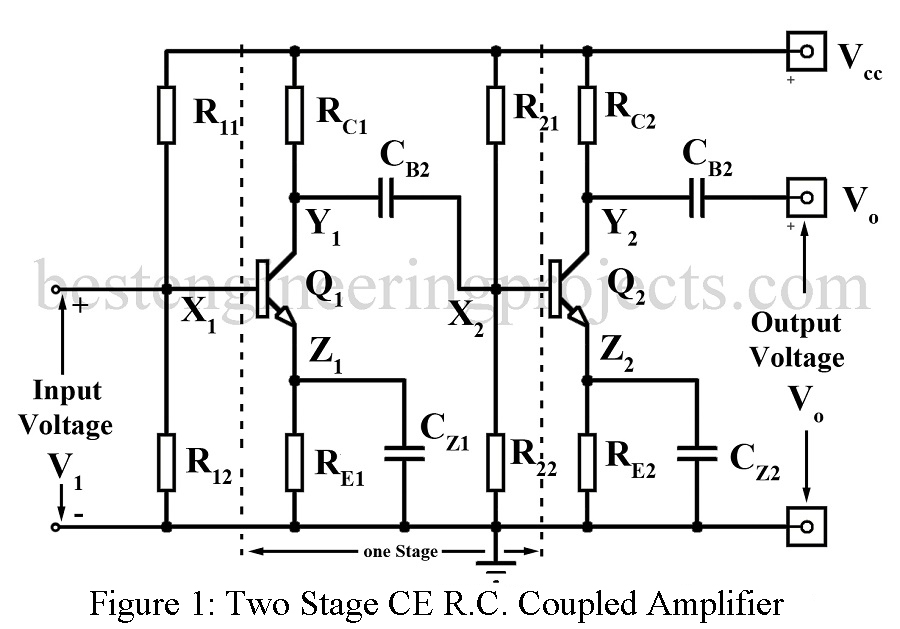
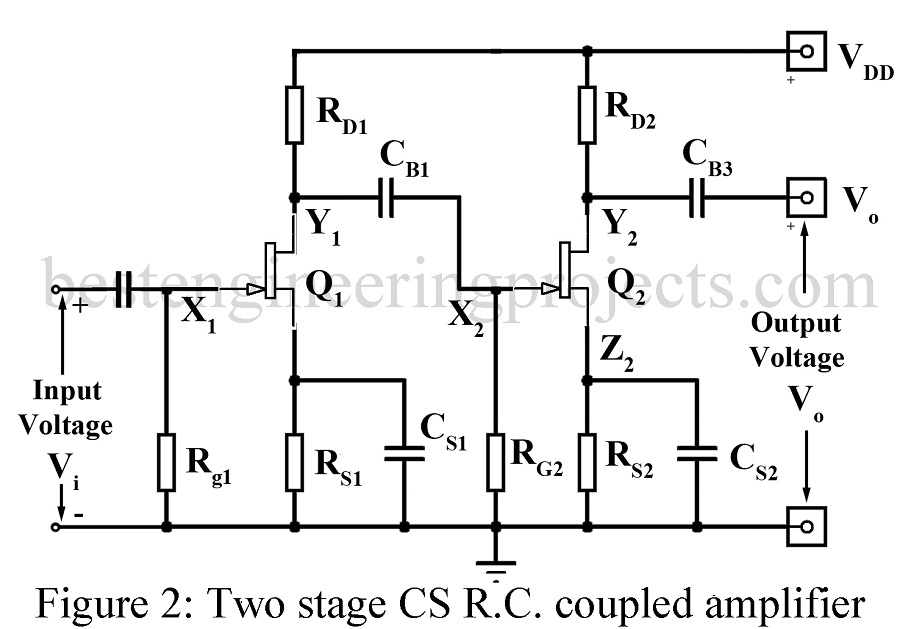
Figure 1 gives the circuit of a two-stage common emitter R.C. coupled amplifier while figure 2 gives the circuit of a two-stage common source (CS) FET R.C. coupled amplifier. Typical component values are also indicated.

In both amplifier circuits of Figure 1 and 2, X₁ and Y₁ are the input and output terminals of the first stage. The output at Y₁ is coupled to the input X₂of the second stage through a coupling capacitor C_b2. This capacitor serves another function of blocking the dc component at Y₁ from reaching X₂. Resistor R_c (R_d) forms the load resistor in the collector (drain) circuit. In the figure 2, R_g1 extends from gate to the ground. This resistor together with R_s1-C_s1 provides the desired bias. In figure 3, emitter circuit resistor R_e1 along with potential divided resistor R₁₁ and R₁₂ provides the desired emitter bias.

In figure 1 and 2, high value bypass capacitor C_Z1 (C_S1) offers an almost short circuit even to the lowest frequency component and thus prevent loss of amplification due to negative feedback. The high frequency response of the amplifier depends on (i) junction capacitance (ii) capacitances associated with the device sockets and proximity of the components to the chassis and (iii) signal leads. For the purpose of analysis, we assume that the active device (BJT or FET) functions linearly permitting use of small signal models.

Frequency Response | Resistance Capacitance Coupled or R.C. Coupled Amplifier

For the purpose of analysis, we may replace the amplifying device (BJT or FET) by its small signal equivalent circuit and then resort to the technique of network analysis.

The entire frequency range may be divided into following three categories:

(a) low frequency range (b) Middle frequency range or midband (c) High frequency range

In the midband, the voltage gain A_Vm, current gain A_Im and phase delay remain almost constant. The low frequency range lies below the midpoint and, in this range, analysis may be done on replacing the transistor (or FET) by its small signal low frequency model. Shunt capacitance may be neglected in the low frequency range.

The high frequency range lies above the midband and in the frequency, the analysis may be done on replacing the transistor (or FET) by its small signal high frequency model. The junction capacitances of the device and so also the stray shunt capacitance have to be considered in the analysis. However, the coupling capacitor C_b may be neglected.

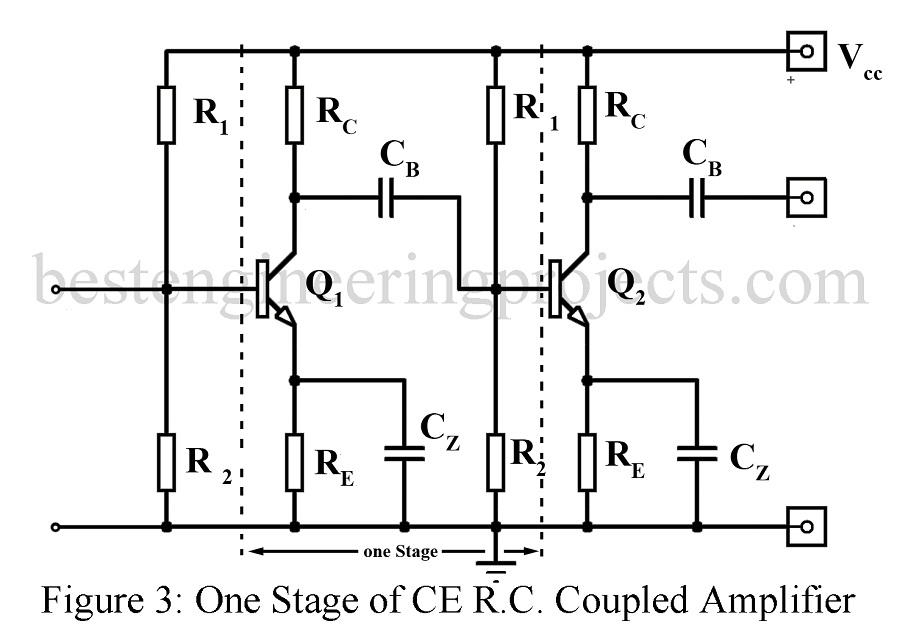
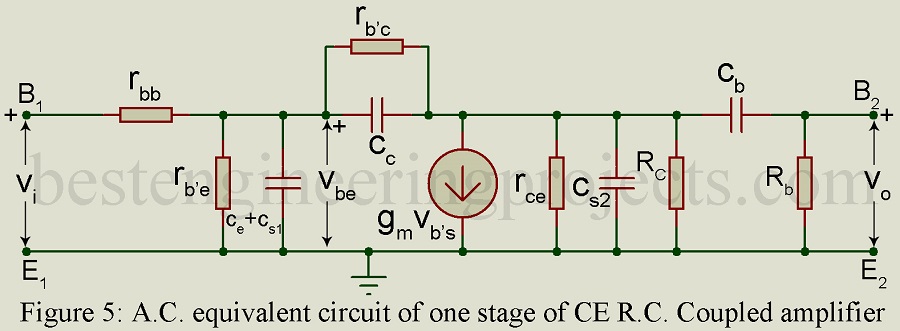
One stage of a multistage BJT amplifier is generally taken from the input i.e. base of one BJT to the base of the BJT in the next stage as shown in figure 1 reproduced in figure 3.

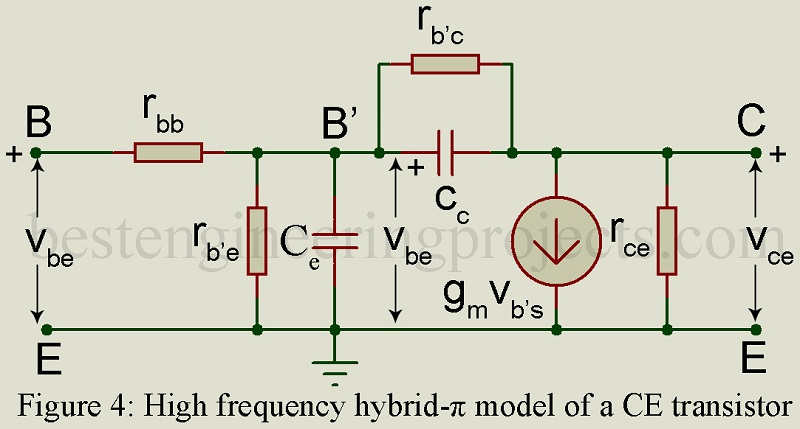
Analysis may be done using an a.c. equivalent circuit for BJT. The circuit most popularly used today is the high frequency hybrid- $\pi$ model for the BJT shown in figure. here r_bb’ is the base spreading resistance and B’ is the internal base.

On replacing BJT in figure 3 by the high frequency hybrid- $\pi$ model of figure 4, the high frequency equivalent circuit for one stage of RC coupled amplifier may be drawn as in figure 5 C_S1 and C_S2 represent the stray capacitances as may be caused by wiring, proximity (closeness) of components to chassis etc.

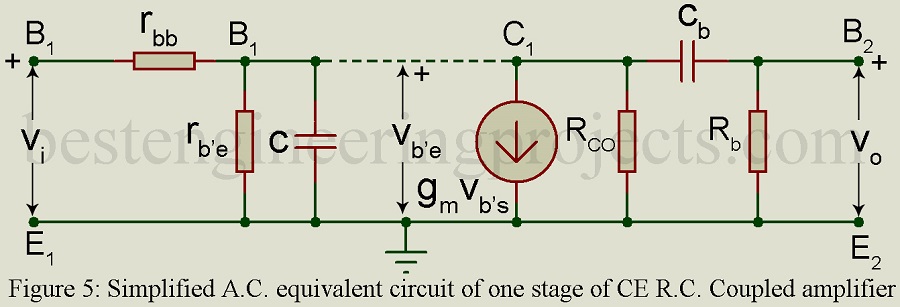
Equivalent circuit of figure 5 is modified using simplifying assumptions and ultimately, we arrive at the amplified a.c. equivalent circuit shown in figure 6.

In figure 7, C represents the total effective shunt capacitance on the input side and is given by,

$C = C_e + C_{S1} + C_c(1 + g_mR_{co})$ …..(1)

$R_{co} = R_c || R_o = \dfrac{R_cR_o}{R_c+R_o}$ ……(2)

Where R_o represent r_ce and approximately equals $\dfrac{1}{h_{oe}}$

$R_b = R_1 || R_2 = \dfrac{R_1R_2}{R_1+R_2}$ …..(3)

Analysis (not taken up here) of this one stage of RC coupled amplifier using equivalent circuit of Figure 6 gives the following results:

(A) Middle Frequency Range (Mid-band)

Current gain $A_{Im} = -h_{fe}\times \dfrac{R_{co}}{R_{co}+R_b}$ …..(4)

Voltage gain $A_{Vm} = \dfrac{h_{fe}}{h_{e}}\times R_{cob}$ …..(5)

Where R_cob is parallel combination of R_co and R_b and equals $R_{co}\times \dfrac{R_b}{R_{co}+R_b}$

From equation (4) and (5) we find that the current gain A_Im and the voltage A_Vm are constant in the middle frequency range.

(B) Low Frequency Range:

In the low frequency range, frequency begin small, reactance of shunt capacitor C is extremely large. Hence C may be omitted from the equivalent circuit of Figure 7. But the reactance of coupling capacitor C_b is quite large. Hence C_b cannot be omitted. In fact, it is the presence of C_b which cause reduction of gain in the low frequency range.

Current gain $A_{IL} = \dfrac{A_{Im}}{1-j(\dfrac{f_L}{f})}$ …..(6)

Where $f_L = \dfrac{1}{2\pi C_b(R_{co} + R_b)}$ …..(7)

Magnitude $A_{IL} = \dfrac{A_{Im}}{\sqrt{1+(\dfrac{f_L}{f})^2}}$ …..(8)

Phase angle of current gain at any frequency f is,

$f_{IL} = 180^0 + arc tan(\dfrac{f_L}{f})$ …..(9)

$=180^0 + arc tan\dfrac{1}{2\pi f C_b(R_{co} + R_b)}$ …..(10)

At $f = f_L, A_{IL} = \dfrac{A_{Im}}{\sqrt{2}} = 0.707 A_{Im}$ . Thus at f_L A_IL is 3 dB below A_Im.

Hence f_L forms the lower 3-dB or lower half power frequency for current gain.

Voltage gain $A_{VL} = \dfrac{A_{VM}}{1-j(\dfrac{f_L}{f})}$ …..(11)

Where $f_L = \dfrac{1}{2\pi C_b (R_{co} + R_b)}$ …..(12)

Magnitude $|A_{VL}| = \dfrac{A_{Vm}}{\sqrt{1 + (\dfrac{F_L}{f})^2}}$ …..(13)

Phase angle $\phi_{VL} = 180^0 + arc\ tan (\dfrac{f_L}{f})$ …..(14)

$= 180^0 + arc\ tan \dfrac{1}{2\pi f C_b(R_{co}+R_b)}$ ……(15)

Thus lower 3-dB frequency for current is the same as the lower 3-dB frequency for voltage gain.

(c) High frequency range:

In the high frequency range, frequency being large, reactance of the coupling capacitance C_b is extremely small. Hence C_b may be omitted. However, reactance of shunt capacitance C is quite small. But C cannot be neglected. In fact, C, being in the shunt path, causes drop in current gain and voltage gain in high frequency range.

Current Gain $A_{Ih} = \dfrac{A_{Im}}{1-j(\dfrac{f}{f_{Ih}})}$ ……(16)

Where, $F_{Ih} = \dfrac{1}{2\pi C R_{\acute{b}e}}$ (17)

Magnitude $|A_{Ih}| = \dfrac{A_{Im}}{1 + (\dfrac{f}{f_{Ih}})^2}$ …..(18)

Phase angle of current gain at any frequency f is,

$f_{Ih} = 180^0-arc\ tan(\dfrac{f}{F_{Ih}})$ …..(19)

$=180^0-arc\ tan(2\pi f C r_{\acute{b}e})$ ……(20)

At f = f_Ih = $A_{Ih} = \dfrac{A_{Im}}{\sqrt{2}}$ = 0.707 A_{Im}[/latex].

Thus, f_Ih forms the higher 3-dB frequency for current gain.

Voltage Gain $A_{vh} = \dfrac{A_{vm}}{1-j(\dfrac{f}{f_{vh}})}$ …..(21)

Where $f_{vh} = \dfrac{1}{2\pi C r_{b\acute{b}e}}$ ……..(22)

Where $r_{b\acute{b}e} = r_{b\acute{b}}|| r_{\acute{b}e} = \dfrac{r_{b\acute{b}} \times r_{\acute{b}e}}{r_{b\acute{b}}+ r_{\acute{b}c}}$ …..(23)

Magnitude $|A_{Vh}| = \dfrac{A_{vm}}{1-j(\dfrac{f}{f_{vh}})^2}$ …..(24)

Phase angle of voltage gain A_vh at any frequency f is,

$\phi_{Vh} = 180^0-arc\ tan\ (\dfrac{f}{f_{vh}})^2$ …..(25)

$= 180^0 -arc\ tan\ (2\pi f C r_{b\acute{b}e})$ ……..(26)

At $f = f_{vh} = \dfrac{A_{vm}}{<2} = 0.707 A_{vh}$ .

Thus, A_vh forms the higher 3-dB frequency for voltage gain.

Frequency Response Curve

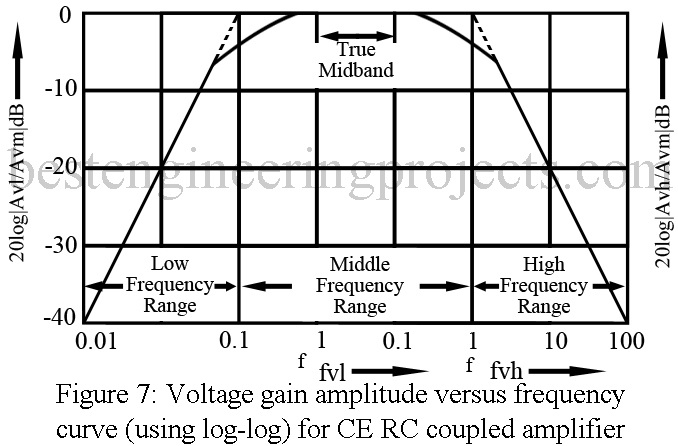
Figure 7 gives the voltage gain versus frequency curve for one stage of CE RC coupled amplifier in the low, middle and high frequency ranges. This forms the frequency response curve. Actually the gin $\dfrac{A_{VL}}{A_{Vm}}$ or $\dfrac{A_{vh}}{A_{vm}}$ expressed in decibels i.e. $20 log |\dfrac{A_{VL}}{A_{vm}}|$ and $20 log |\dfrac{A_{vh}}{A_{vm}}|$ are plotted along the y-axis on linear scale against frequency f on log scale. Thus, effectively the gain versus frequency is plotted on log-log scale. Thus, curve is called the Bode magnitude plot.

Bandwidth 3-dB bandwidth: or simply the bandwidth B of an amplifier is the frequency range extended from lower 3-dB frequency f_VL to higher 3-dB frequency f_vh. In this frequency range, the magnitude of the gain remains almost constant ignoring the 3-dB variation. In most cases f_vh >> f_vL. Hence, Bandwidth B = f_vh– f_vL = f_vh

True Mid-band true midband extends for 10 f_vL to 0.1 f_vh in which frequency range, gain A_v remains truly constant.

If we plot | $\dfrac{A_{IL}}{A_{Im}}$ | or | $\dfrac{A_{Ih}}{A_{Im}}$ | in dB against frequency f on log scale, again we arrive at the curve in Figure 10.11. Corresponding 3-dB bandwidth is then,

$B = F_{Ih}-F_{Il} = F_{Ih}$ ……(27)