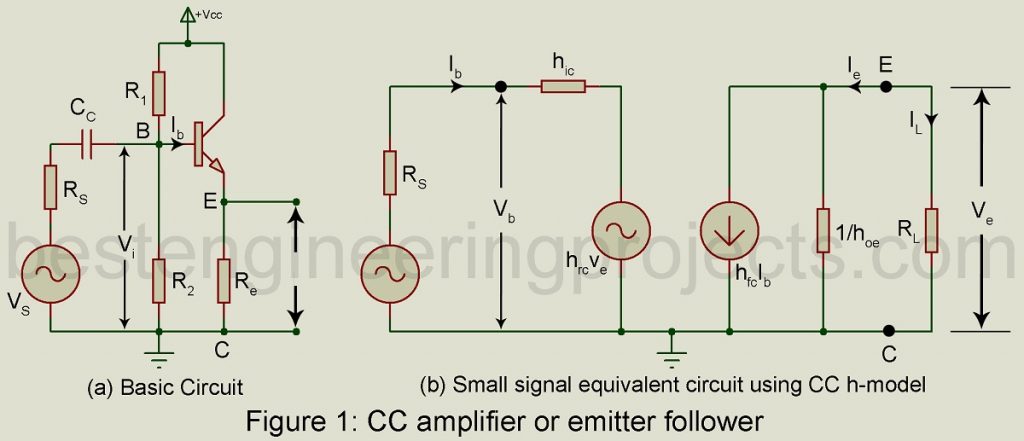
Common Collector Amplifier or the Emitter Follower

Common Collector Amplifier or the Emitter Follower: Figure 1(a) gives the basic circuit of a common collector amplifier, popularly called emitter follower. Its voltage gain is close to unity (one) and, therefore, any increment in the input voltage i.e. the base voltage appears as an equal increment in the output voltage across the load resistor in the emitter circuit.

Thus, the emitter may be said to follow the input signal and hence the name emitter follower. The input resistance R_i of a CC amplifier or emitter follower is very high, of the order of hundred of kilo-ohms while its output resistance is very low, of the order of tens of ohms. High R_i and low R₀ permits us to use emitter follower as an impedance matching stage to match the high output impedance of one amplifier stage to the low input impedance of the next stage over a wide frequency range. With voltage gain very close to but slightly less than unity, the emitter follower serves the function of resistance transformation. Further emitter follower increases the power level of the signal since its current gain A_I is quite large.

Analysis of Common Collector Amplifier or the Emitter Follower

Figure 1(b) gives the small signal equivalent circuit of the emitter follower of figure 1(a) on

Omitting dc voltage source
Omitting the biasing resistor R₁ – R₂ and the coupling capacitor C_C and
Replacing the transistor by its small signal two generator h-parameter model.

Here also we assume sinusoidal input signal. Hence in the equivalent circuit, we have used rms values of voltages and currents nearly I_b, V_b, I_e, V_e.

The equivalent circuit of figure 1(a) is similar to that of CE amplifier of Figure 2. Hence the analysis procedure is exactly the same. The expression of A_I, R_i, A_V, A_IS, A_VS and Y₀ are, therefore, the same as of CE amplifier except that h-parameters of CC configuration are used. We may make use of Table 1 and simultaneously use conversion Table 2 to get the expression for A_I, R_i, A_V and R₀.

Table 1: Result of small single analysis of low frequency cc amplifier
$A_I = -\dfrac{h_{fe}}{1+h_{oe}\times R_L}$	$A_V = \dfrac{A_I\times R_L}{R_i}$
$R_i = h_{ie} + h_{re}\times A_I \times R_L$	$A_{VS} \dfrac{A_{V}R_i}{R_i + R_s}$
$Y_0 = h_{oe}-\dfrac{h_{re}h_{fe}}{h_{ie}+R_s} = \dfrac{1}{Z_0}$	$A_{IS} = \dfrac{A_I R_s}{R_i + R_s}$

Table 2 Approximate Conversion Formulas for h-parameter
$h_{ic} = h_{ie}$	$h_{ib} = \dfrac{h_{ie}}{1+h_{fe}}$
$h_{fc} = (1+ h_{fe})$	$h_{fb} = -\dfrac{h_fe}{1+h_{fe}}$
$h_{rc} = 1$	$h_{rb} = \dfrac{h_{ie}\times h_{oe}}{1+h_{fe}}-h_{re}$
$h_{oc} = h_{oe}$	$h_{ob} = \dfrac{h_{oe}}{1+h_{fe}}$

Thus, from Table 1 and Table 2,

Current gain $A_I = -\dfrac{I_e}{I_b} = -\dfrac{h_{fc}}{1 + h_{oc} \times R_L} = \dfrac{1 + h_{fe}}{1 + h_{oe} \times R_L}$ …..(1)

Input resistance $R_i = \dfrac{V_i}{I_b} = h_{ic} + h_{re}\times A_I \times R_L = h_{ie} + A_I \times R_L$ …..(2)

Voltage gain $A_V = \dfrac{V_e}{V_i} = \dfrac{A_I \times R_L}{R_i}$ …..(3)

But from equation (2) $A_I \times R_L = R_i-h_{ie}$

Hence $A_V = \dfrac{R_i-h_{ie}}{R_i} = 1-\dfrac{h_{ie}}{R_i}$ …..(4)

Overall voltage gain $A_{VS} = \dfrac{A_V \times R_i}{R_i + R_s}$ …..(5)

Overall current gain $A_{IS} = \dfrac{A_I \times R_s}{R_i + R_s}$ …..(6)

Output admittance $Y_0 = h_{oc}-\dfrac{h_{fc}\times h_{rc}}{h_{ic} + R_s} = h_{oe} + \dfrac{1 + h_{fe}}{h_{ie} + R_s}$ ……(7)

Power gain $A_P = A_I \times A_V$ …..(8)

Example 1 A transistor amplifier in CC configuration is driven by a voltage source V_s of internal resistance R_s = 1000 $\Omega$ . The load impedance is a resistor R_L = 4000 $\Omega$ . The h-parameters are: $h_{ic} = 1100\Omega$ , h_fc = -51 and $h_{oc} = 25\mu S$ . Calculate for this amplifier, the current gain A_I, input resistance R_i, voltage A_V, overall voltage gain A_VS, overall current gain A_IS, output resistance R₀ and power gain A_P.

Solution:

Current gain $A_I = \dfrac{-h_{fc}}{1 + h_oc \times R_L} = \dfrac{(-(-51))}{1 + (25 \times 10^{-6}\times 4000)} = 46.4$

Input Resistance $R_i = h_{ic} + h_{rc} \times A_I \times R_L = 1100 + (1 \times 46.4 \times 4000)\Omega = 186.7 l\Omega$

Voltage gain $A_V = \dfrac{A_I\times R_L}{R_i} = \dfrac{46.4 \times 4000}{186.7 \times 10^3} = 0.994$

Overall Voltage gain $A_{VS} = \dfrac{A_V \times R_i}{R_i + R_s} = \dfrac{0.994 \times 186.7 \times 10^3}{(186.7 + 1) 10^3} = 0.989$

Overall current gain $A_{IS} = \dfrac{A_I \times R_s}{R_i + R_s} = \dfrac{46.5 \times 1000}{(186.7 + 1)\times 10^3} = 0.247$

Output admittance $Y_0 = h_{oc}-\dfrac{h_{fc}\times h_{rc}}{h_{ic} + R_S} = (25 \times 10^{-6})-\dfrac{(-51)\times (1)}{1100 + 1000} = 24.31 \times 10^{-3}S$

Output resistance $Z_0 = \dfrac{1}{Y_0} = \dfrac{1000}{24.31} = 41.1 \Omega$

Power gain $A_P = A_V \times A_I = 0.994 \times 46.4 = 46.1$

Analysis of Common Collector Amplifier or the Emitter Follower

Table 1: Result of small single analysis of low frequency cc amplifier

Table 2 Approximate Conversion Formulas for h-parameter

Share this:

Leave a Comment Cancel reply