Importance of High Percentage Modulation

What is the Importance of High Percentage Modulation?

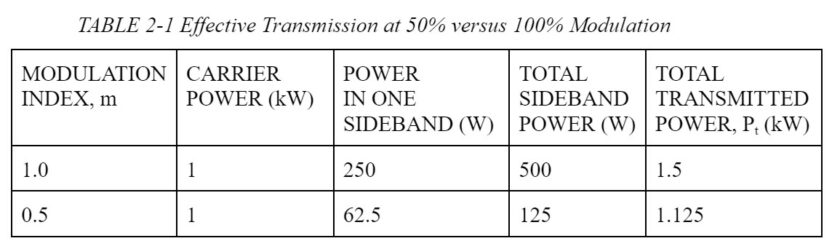
It is important to use as high a percentage modulation as possible while ensuring that overmodulation does not occur. The sidebands contain the information and have maximum power at 100% modulation. For example, if 50% modulation were used, the sideband amplitudes are ¼ the carrier amplitude, and since power is proportional to E2, we have (¼)2, or 1/16 the carrier power. Thus, total sideband power is now 1/16 x 1 kW x 2, or 125 W. The actual transmitted intelligence is thus only ¼ of the 500 W sideband power transmitted at full 100% modulation. These results are summarized in Table 2-1. Even though the total transmitted power has only fallen from 1.5 kW to 1.125 kW, the effective transmission has only ¼ the strength at 50% modulation as compared to 100%. Because of these considerations, most AM transmitters attempt to maintain between 90 and 95% modulation as a compromise between efficiency and the chance of drifting into overmodulation. A valuable relationship for many AM calculations is

$P_t = P_C(1 + \dfrac{m^2}{2})$ (Eq. 1)

where Pt = total transmitted power (sidebands and carrier)

PC = carrier power

m = modulation index

Figure 1: Comparison table

Equation (1) can be manipulated to utilize current instead of power. This is a useful relationship since current is often the most easily measured parameter of a transmitter’s output to the antenna.

[I_t = I_C\sqrt{1+\dfrac{m^2}{2}}][/latex] (Eq. 2)

where It, = total transmitted current

IC = carrier current

m = modulation index

Equation (2) can also be used with E substituted for $I(E_t = E_C \sqrt{1 + \dfrac{m^2}{2}})$ .

EXAMPLE 1: A 500-W carrier is to be modulated to a 90% level. Determine the total transmitted power.

Solution:

$P_t = P_C(1 + \dfrac{m^2}{2})$

$500 W = P_C(1+\dfrac{0.9^2}{2})$

$= 702.5 W$

EXAMPLE 2: An AM broadcast station operates at its maximum allowed total output of 50 kW and at 95% modulation. How much of its transmitted power is intelligence (sidebands)?

Solution:

$P_t = P_C(1 + \dfrac{m^2}{2})$

$50 kW = P_C(1+\dfrac{0.95^2}{2})$

$P_C = \dfrac{50 kW}{1 + (\dfrac{0.95^2}{2})}$

$= 34.5 kW$

Therefore, the total intelligence signal is

$P_i = P_t - P_C = 50 kW-34.5kW = 15.5 kW$

EXAMPLE 3: The antenna current of an AM transmitter is 12 A when unmodulated but increases to 13 A when modulated. Calculate %m.

Solution:

$I_t = I_C\sqrt{1+\dfrac{m^2}{2}}$

$13A = 12A \sqrt{1 + \dfrac{m^2}{2}}$

$1+\dfrac{m^2}{2} = (\dfrac{13}{12})^2$

$m^2 = 2[(\dfrac{13}{12})^2-1]$

= 0.34

m = 0.59

%m = 0.59 x 100% = 59%

EXAMPLE 4: An intelligence signal is amplified by a 70% efficient amplifier before being combined with a 10-kW carrier to generate the AM signal. If it is desired to operate at 100% modulation, what is the dc input power to the final intelligence amplifier?

Solution:

You may recall that the efficiency of an amplifier is the ratio of ac output power to dc input power. To fully modulate a 10-kW carrier requires 5 kW of intelligence. Therefore, to provide 5 kW of sideband (intelligence) power through a 70% efficient amplifier requires a dc input of

$\dfrac{5 kW}{0.70} = 7.14 kW$

If a carrier is modulated by more than a single sine wave, the effective modulation index is given by

$m_{eff} = \sqrt{m_1^2 + m_2^2 + m_3^2}$

The total effective modulation index must not exceed 1 or distortion (as with a single sine wave) will result. The term meff can be used in all previously developed equations using m.

EXAMPLE 5: A transmitter with a 10-kW carrier transmits 11.2 kW when modulated with a single sine wave. Calculate the modulation index. If the carrier is simultaneously modulated with another sine wave at 50% modulation, calculate the total transmitted power.

Solution:

R-P(1+)

$P_t = P_c(1+\dfrac{m^2}{2})$