Common Drain Amplifier using FET - Engineering Projects

Common Drain Amplifier Introduction

In the common drain amplifier, the input signal is applied between the gate and drain and the amplified output voltage is developed across a resistor in the source-to-drain circuit. The drain is the terminal common to the input and the output sides.

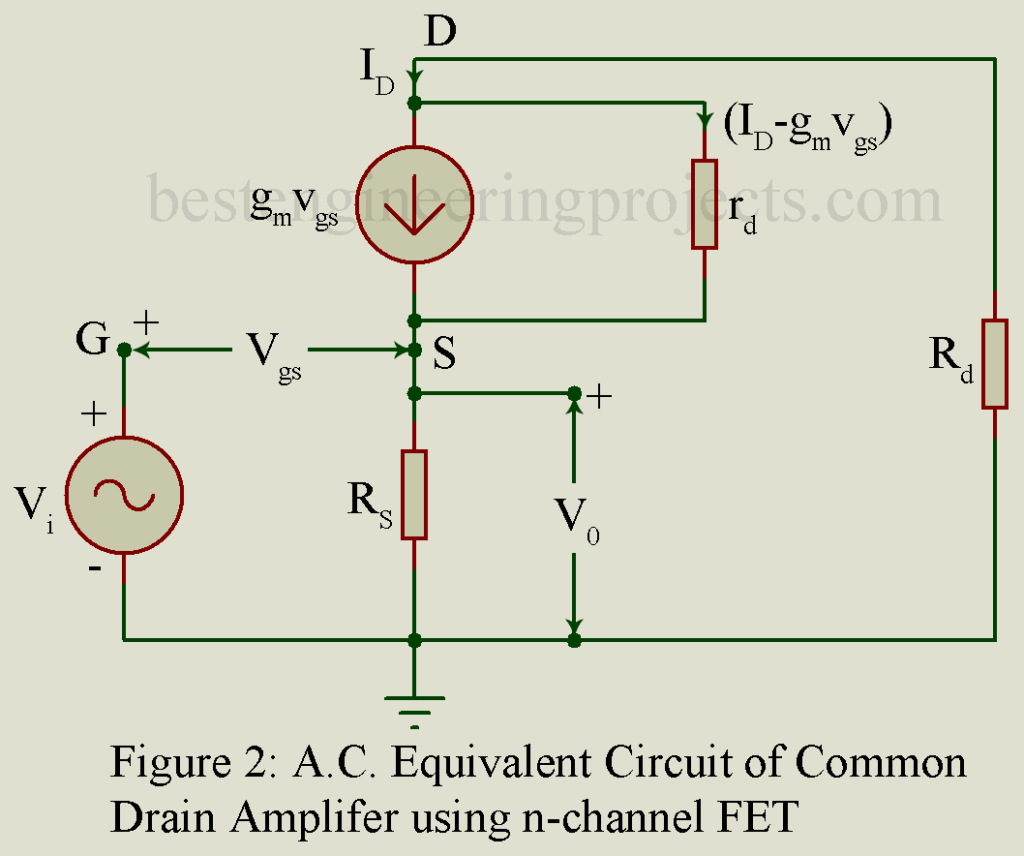
Figure 1 gives the circuit of one stage of a common drain amplifier (CD) using n-channel FET. R_s is the load impedance placed in the source circuit. Quite often a resistor R_d is placed in the drain circuit to further stabilize the operation of the amplifier. However, the use of the same is not essential. This circuit is analogous to the common collector (CC) amplifier. On using p-channel FET, the polarity of the supply voltage is reversed.

Analysis of Common Drain Amplifier (CD)

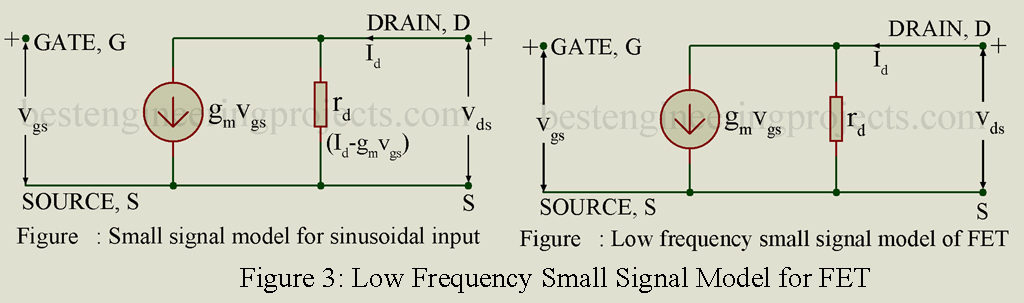
Resistor R provides the self-bias also. No gate current follows. Hence, the input impedance is infinity. The analysis given here applies to both the n-channel and p-channel Common drain amplifiers. Figure 2 gives the small signal low-frequency equivalent circuit. Here FET has been replaced by its small signal low-frequency model of figure 3.

On applying KVL to the output circuit we get,

$I_d \times R_d + I_d \times R_s + (I_d-g_m \times V_{gs})\times r_d =0$ …….(1)

But from the figure 2,

$V_{gs} = V_i-I_dR_s$ ……..(2)

On substituting the value of V_gs from equation 2 into equation 1 and rearranging we get,

Hence,

$I_d = \dfrac{\mu \times V_i}{r_d + R_d + (\mu + 1)R_s}$ ……..(3)

Hence output voltage,

$V_o = I_dR_s = \dfrac{\mu V_i R_s}{r_d + R_d + (\mu + 1)R_s}$ …….(4)

Hence voltage gain,

$A_v = \dfrac{V_o}{V_i} = \dfrac{\mu \times R_s}{r_d + R_d + (\mu + 1)R_s}$ …….(5)

Evidently, the output voltage V_o is in phase with the input voltage V_i. But the voltage gain is always less than one.

Equation 4 may be put as, $V_o = \dfrac{\dfrac{\mu V_i}{\mu + 1}R_s}{\dfrac{r_d + R_d}{\mu + 1}+ R_s}$ ………(6)

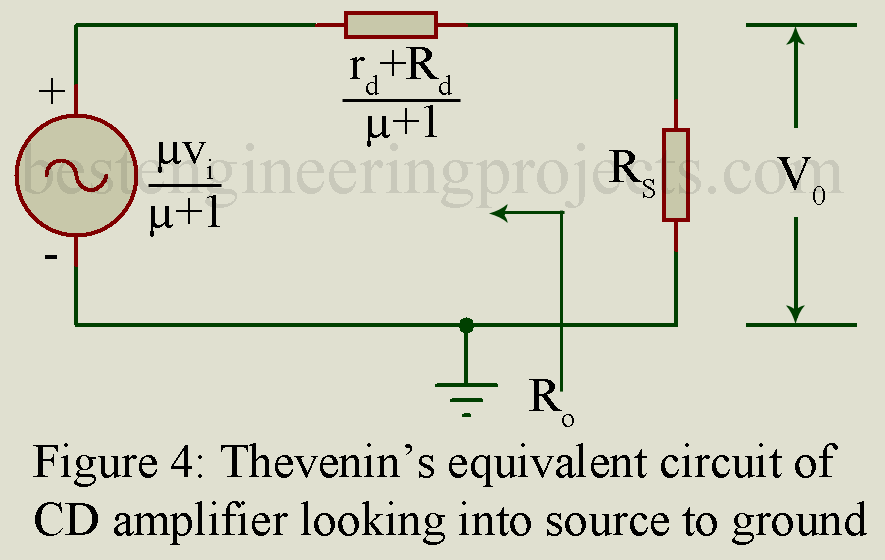
Figure 4 gives the equivalent circuit, called Thevenin’s equivalent circuit, looking from the load resistor R_s into the source S to ground N. This circuit is obtained from equation (6).

From figure 4, the output impedance R_o is given by,

$R_o = \dfrac{r_d + R_d}{\mu + 1}$ ……..(7)

With R_d = 0 In case of R_d is omitted, we get,

$R_o = \dfrac{r_d}{\mu + 1}$ ………(8)

Hence,

$g_o = \dfrac{1}{R_o} = \dfrac{\mu + 1}{r_d} \approx \dfrac{\mu}{r_d} = g_m$ …….(9)

Also, voltage gain,

$A_v = \dfrac{\mu R_s}{r_d + (\mu + 1)R_s}$ ………(10)

If $(\mu + 1)R_s$ >> $r_d$ , then

$A_v = \dfrac{\mu R_s}{(\mu + 1)R_s} = \dfrac{\mu}{\mu + 1}$ ……..(11)

Numerical Example of Common Drain Amplifier

Example 1: A common drain amplifier uses FET having dynamic drain resistance r_d = 200 k-ohm and $\mu$ = 20. Calculate the output impedance and voltage gain for the following values of load resistor R_s : (i) 200 $k\Omega$ (ii) 400 $k\Omega$ (iii) 600 $k\Omega$ .

Solution:

$R_o = \dfrac{r_d}{\mu + 1}$ ;

$A_v = \dfrac{\mu R_s}{r_d + (\mu + 1)R_s}$

Given:

$\mu = 20$ ; $r_d = 200 k\Omega$ ,

$R_0 = \dfrac{200 k\Omega}{(20 + 1)} = 9.52 k\Omega$

For $R_s = 200 k\Omega$ : $A_v = \dfrac{20 \times 200}{200 + (20 + 1)200} = 0.909$
For $R_s = 400 k\Omega$ : $A_v = \dfrac{20 \times 400}{200 + (20 + 1)400} = 0.93$
For $R_s = 600 \Omega$ : $A_v = \dfrac{20 \times 600}{200 + (20 + 1)600} = 0.937$

Example 2: A common drain amplifier uses FET having $\mu = 24$ and dynamic drain resistance $r_d = 200 k\Omega$ . A resistor $R_d = 50 k\Omega$ is placed in the drain circuit. Calculate the voltage gain A_v and the output resistance R₀ for the following values of load resistor R_s in the source circuit: (i) $200 k\Omega$ (ii) $300 k\Omega$ (iii) $400 k\Omega$

Solution: $Z_0 = \dfrac{r_d + R_d}{\mu + 1} = \dfrac{(200 + 50)10^3}{24 + 1}\Omega = 10 k\Omega$

Voltage gain $A_v = \dfrac{\mu R_s}{r_d + R_d + (\mu + 1) R_s}$

For $R_s = 200 k\Omega$ , $A_v = \dfrac{24 \times 200}{200 + 50 + (24 + 1)200} = 0.914$
For $R_s = 300 k\Omega$ , $A_v = \dfrac{24 \times 300}{200 + 50 + (24 + 1)300} = 0.929$
For $R_s = 400 k\Omega$ , $A_v = \dfrac{24 \times 400}{200 + 50 + (24 + 1)400} = 0.9366$

Tutorial Problem 1 (a) Draw the circuit of a common drain amplifier with a resistor R_d in the drain circuit. Draw its small signal equivalent circuit and drive expression for the voltage gain A_v and the output resistance R_o. (b) A common drain amplifier uses FET having $r_d = 300 k\Omega$ and $\mu = 30$ . The load resistance $R_s = 200 k\Omega$ . A resistor R_d is placed in the drain circuit. Calculate the voltage gain A_v and output resistance R_o for the following values of R_d: