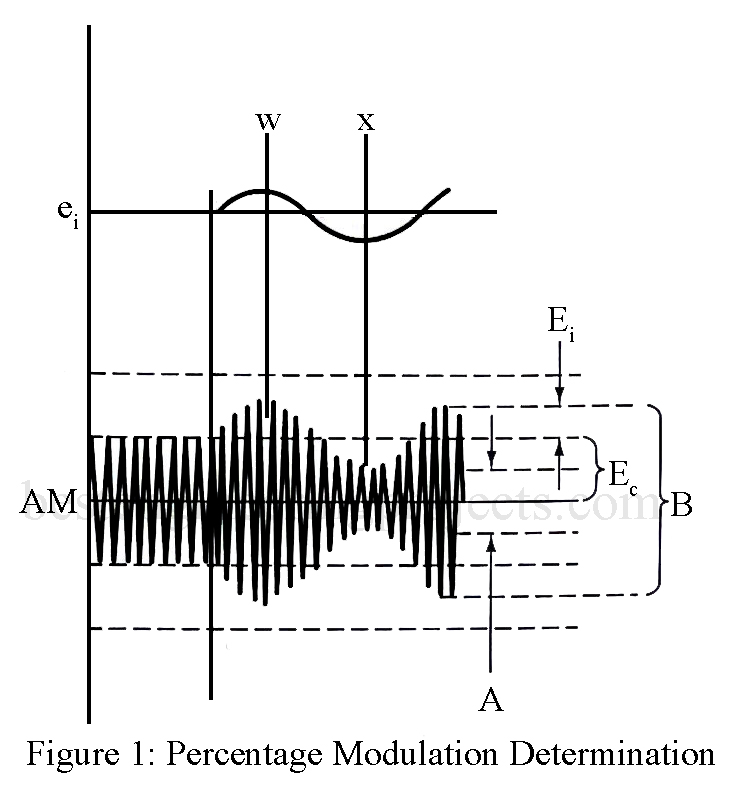
Analysis of Amplitude Modulation

Engineeering Projects

Analysis of Amplitude Modulation

The equation for the amplitude of an AM waveform can be written as the carrier peak amplitude, EC, plus the intelligence signal, ei. Thus, the amplitude E is

E = EC + ei

but e_i = E sin\omega_i t, so that

E = E_C + E_i sin \omega_i t

m = \dfrac{E_i}{E_C}

From the above Equation, Ei = mEC, so that

E = E_C + mE_C sin\omega_i t

= E_C(1 + m sin \omega_it)

The instantaneous value of the AM wave is the amplitude term E just developed times sin\omega_C t. Thus,

e = E sin \omega_c t

= E_c(1 + m sin \omega_it)sin \omega_ct

percentage modulation determination

Notice that the AM wave (e) is the result of the product of two sine waves. This can be expanded with the help of the trigonometric relation sin x sin y = \dfrac{1}{2}[cos(x-y)-cos(x+y)]. Therefore,

e = E_C sin \omega_Ct + \dfrac{mE_C}{2}cos(\omega_c-\omega_i)t-\dfrac{mE_C}{2}cos(\omega_c + \omega_i)t

The preceding equation proves that the AM wave contains the three terms previously listed: the carrier, the upper sideband at f_c + f_i[latex], and the lower sideband at [latex]f_c - f_i[latex]. It also proves that the instantaneous amplitude of the side frequencies is [latex]\dfrac{mE_C}{2}. It shows conclusively that the bandwidth required for AM transmission is twice the highest intelligence frequency.

In the case where a carrier is modulated by a pure sine wave, it can be shown that at 100% modulation, the upper and lower side frequencies are one-half the amplitude of the carrier. In general, as just developed,

E_{SF} = \dfrac{mE_C}{2}

where ESF = side-frequency amplitude

m = modulation index

EC = carrier amplitude

In an AM transmission, the carrier amplitude and frequency always remain constant while the sidebands are usually changing in amplitude and frequency. The carrier contains no information since it never changes. However, it does contain the most power since its amplitude is always at least double (when m = 100%) the sideband’s amplitude. It is the sidebands that contain the information.

Example: Determine the maximum sideband power if the carrier output is 1 kW and calculate the total maximum transmitted power.

Solution

Since

E_{SF} = \dfrac{mE_C}{2}

it is obvious that the maximum sideband power occurs when m = 1 or 100%. At that percentage modulation, each side frequency is ½ the carrier amplitude. Since power is proportional to the square of the voltage, each sideband has ¼ of the carrier power or ¼ x 1kW, or 250 W. Therefore, the total sideband power is 250 W x 2 = 500 W, and the total transmitted power is 1 kW +500 W or 1.5 kW.

Leave a Comment