Two of the most common alphanumeric codes schemes for binary data are ASCII, the American Standard Code for Information Interchange; and EBCDIC, the Extended Binary-Coded Decimal Interchange Code. Each of these codes can be found in many digital systems, with the ASCII code being the most prevalent.
Types of Alphanumeric Codes
The ASCII Code
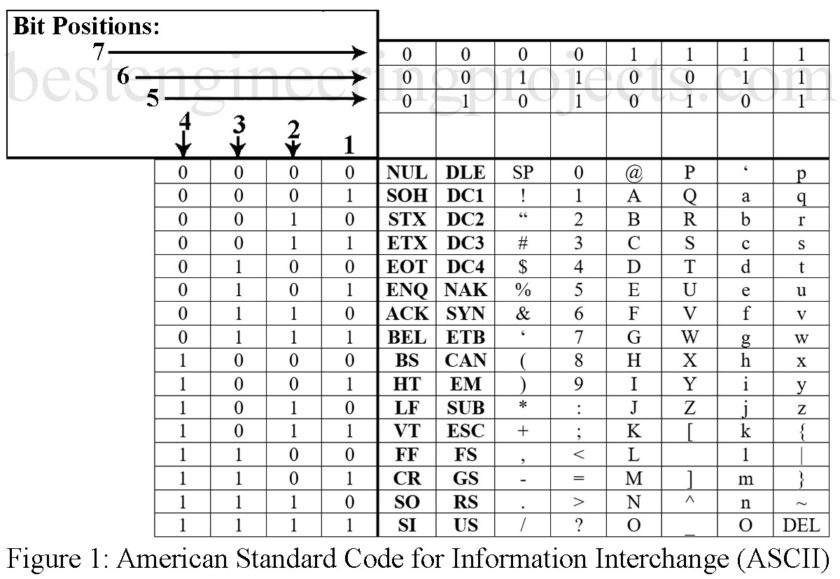
ASCII is a 7-bit code used for representing alpha-numeric symbols with a distinctive code word. The ASCII code was developed by a committee of the American National Standards Institute (ANSI) for the purpose of coding binary data. ASCII-77 is the adopted international standard. Figure 1 provides a list of the codes.
There are 27 (128) possible 7-bit code words available with an ASCII system. The binary codes are ordered sequentially, which simplifies the grouping and sorting of the characters. The 7-bit words are ordered with the least significant bit (LSB) given as bit 1 (b1), while the most significant bit (MSB) is bit 7 (b7). Notice that a binary value is not specified by the code for bit 8 (b8). Usually, the bit 8 (b8) position is used for parity checking. Parity is an error detection scheme that identifies whether an even or odd number of logical ones are present in the codeword. For ASCII data used in a serial transmission system b1, the LSB bit is transmitted first.
Sample of Control Characters (Bold) Examples:
STX = Start to text 1000011 = C
EOT = End of transmission 0110011 = 3
CR = Carriage return 1010000 = P
HT = Horizontal tabulation 0110000 = 0 (Zero)
0100000 = SP (space)
The ASCII system is based on the binary-coded-decimal (BCD) code in the last 4 bits. The first 3 bits indicate whether a number, letter, or character is being specified. Notice that 0110001 represents “1,” while 1000001 represents “A” and 1100001 represents “a.” It uses the standard binary progression (i.e., 0110010 represents “2”), and this makes mathematical operations possible. Since the letters are also represented with the binary progression, alphabetizing is also achieved via binary mathematical procedures. The student should also be aware that analog waveform coding is accomplished simply by using the BCD code for PCM systems.
In some systems, the actual transmission of these codes includes an extra pulse at the beginning (start) and ending (stop) for each character. When the start/stop pulses are used in the coding of signals, it is called an asynchronous (nonsynchronous) transmission. A synchronous transmission (without start/stop pulses) allows more characters to be transmitted within a given sequence of bits. The transmission of information between various computer installations may require the less efficient asynchronous transmitting mode depending on computer characteristics.
The EBCDIC Code | Alphanumeric Codes
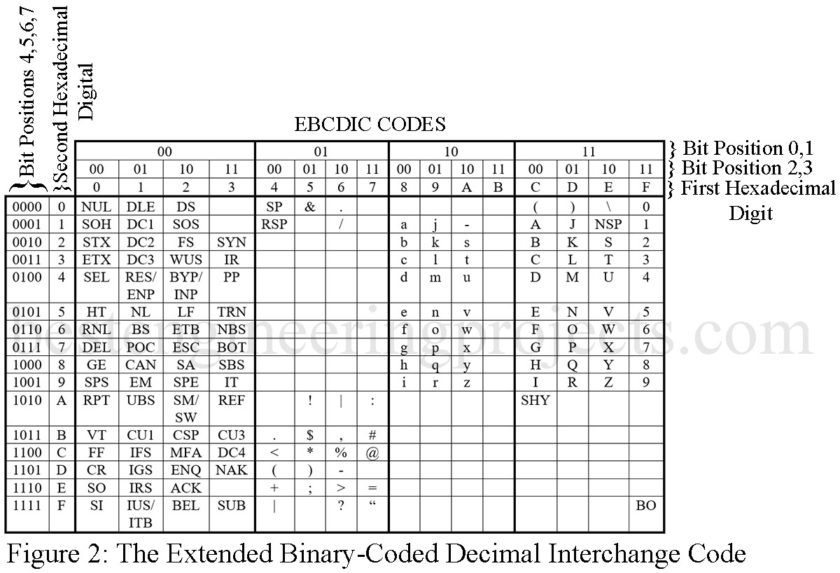
The Extended Binary-Coded Decimal Interchange Code (EBCDIC) is an 8-bit alphanumeric code. The term “binary-coded decimal” is used in the name because of the structure present in the coding scheme, which uses only the 0-9 positions. A list of the code words for the EBCDIC system is given in Fig. 2. and the acronyms for the control characters are listed in Table 1.
Table 1: The EBCDIC Code – List of Acronyms
| ACK Acknowledge
BEL Bell BS Backspace BYP Bypass Presentation INP Inhibit Presentation CAN Cancel CR Carriage Return CSP Control Sequence prefix CU1 Customer Use 1 CU3 Custom Use 3 DC1 Device Control 1 DC2 Device Control 2 DC3 Device Control 4 DC4 Device Control 4 DEL Delete DLE Data Link Escape EM End of Medium ENQ Enquiry EO Eight Ones EOT End of Transmission ESC Escape ETB End of Transmission ETX End of Text FF Form Feed FS Field Separator GE Graphic Escape HT Horizontal Tab IFS Interchange File Sep. IGS Interchange Group Sep. IR Index Return IRS Interchange record Sep. |
NAK Negative Acknowledge
NBS Numeric Backspace NL New Line NUL Null POC Program-Operator Comm. PP Presentation Position RES/NEP Restore/Enable Presentation RFF Required Form Feed RNL Required New Line RPT Repeat SA Set Attribute SBS Subscript SEL Select SFE Start Field Extend SI Shift In SM/SW Set Mode/Switch SO Shift Out SOH Start of Heading SOS Start of Significance SPS Superscript STX Start of Text SUB Substitute SYN Synchronous Idle TRN Transparent UBS Unit Backspace VT Vertical Tab WUS Word Underscore IT Indent Tab IUS Interchange Record Sep. ITB Intermediate Text Block LF Life Feed MFA Modify Field Attribute |
The Baudot Code | Alphanumeric Codes
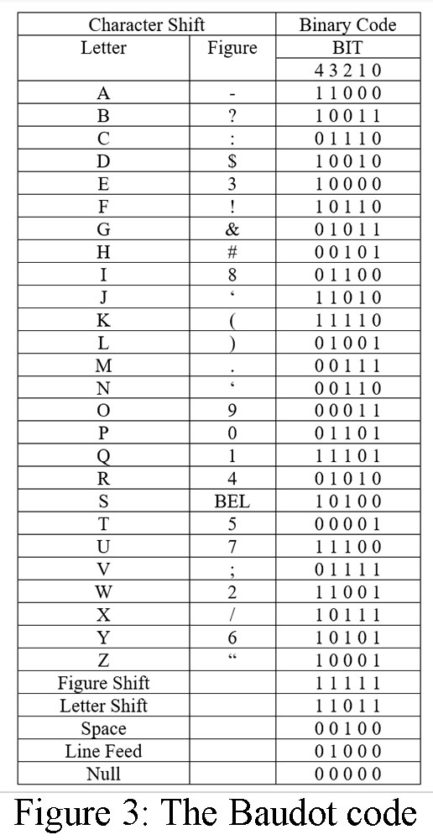
Another interesting code is the Baudot code. The Baudot code was developed in the days of teletype machines such as the ASR-33 Teletype terminal. Baudot is an alpha-numeric code based on five binary values. The Baudot code is not very powerful, but it does have its place in communications history and still can be of use in limited circumstances. The Baudot code is provided in Fig. 3.
The alphabet has 26 letters, and there is an almost equal number of commonly used symbols and numbers. The 5-bit Baudot code is capable of handling these possibilities. A 5-bit code can have only 25 or 32 bits of information but actually provides 26×2 bits by transmitting a 11111 to indicate all following items are “letters” until a 11011 transmission occurs, indicating “figures.” Notice that no provision for lowercase letters is provided.
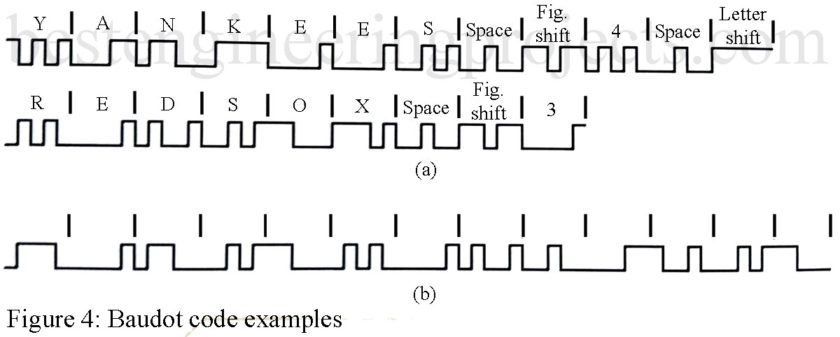
Figure 4(a) shows an example of the Baudot code to transmit “YANKEES 4 REDSOX 3.” Be sure to work out the code in Fig. 4(b) on your own; it is the only “X-rated” part of this article that I was allowed to include.
The Gray Code
The last alpha-numeric code we will look at is the Gray code. The Gray code is a numeric presenting the decimal values from 0 to 9. It is based on the relationship that only one bit in a binary word changes for each binary step. For example, the code for 7 is 0010 while the code for 8 is 0011. Notice that only one binary bit changes when the decimal value changes from 7 to 8. This is true for all of the numbers (0-9). The Gray code is shown in Fig. 5.
The Gray code is used most commonly in telemetry systems that have slow-changing data. This coding scheme works well for detecting errors in slowly changing outputs, such as data from a temperature sensor (thermocouple). If more than one change is detected when words are decoded, then the receiving circuitry assumes that an error is present.