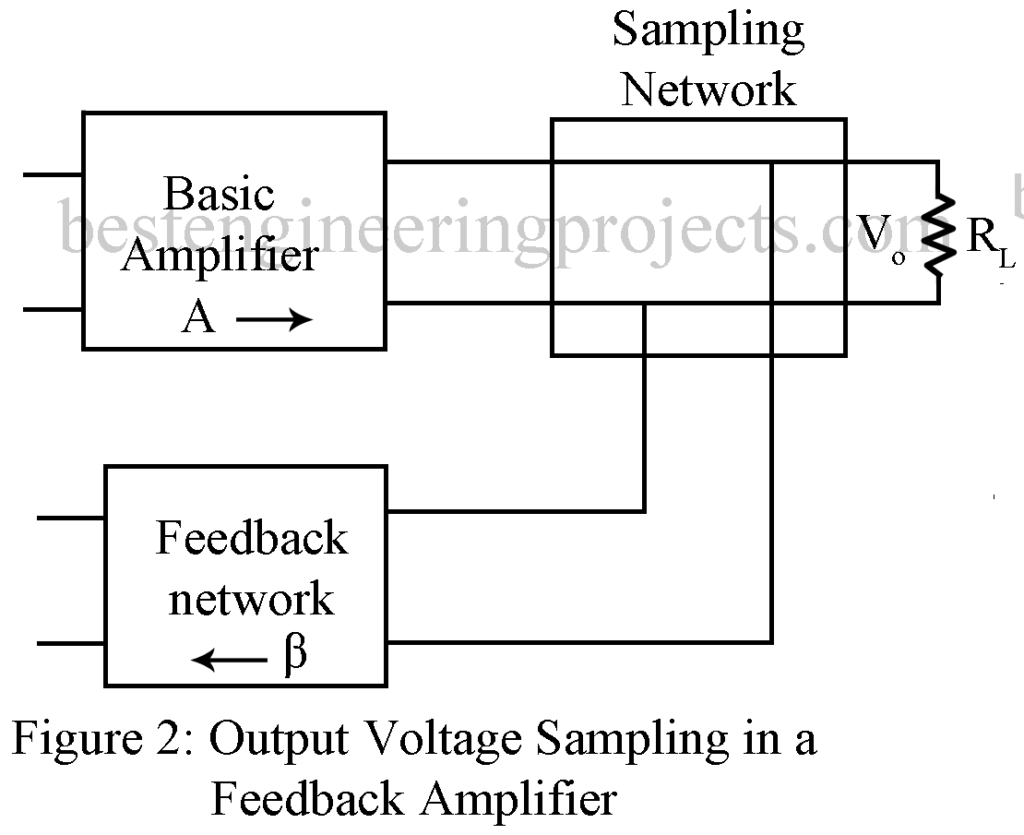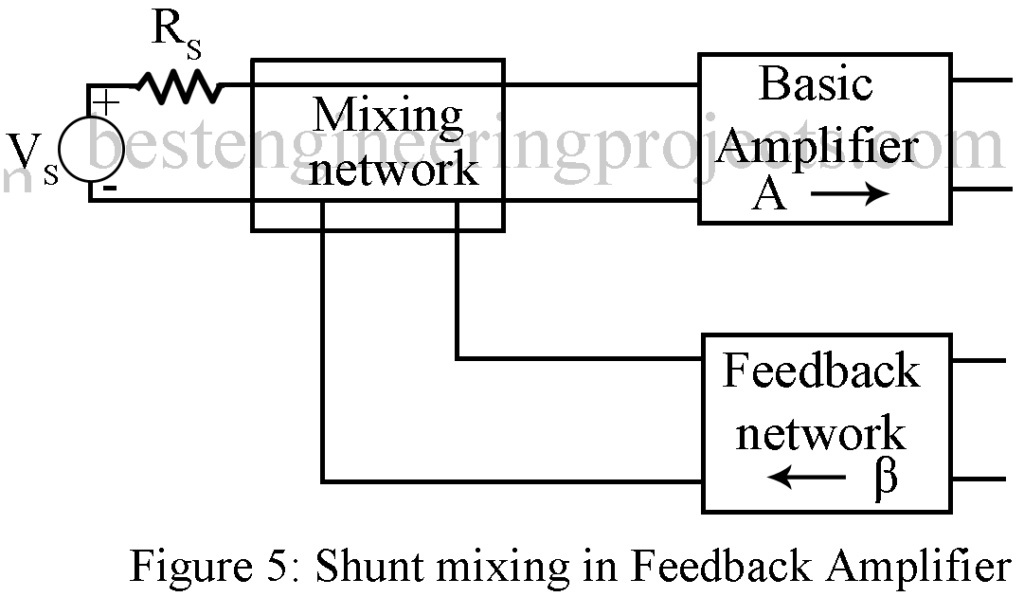Feedback in Amplifiers | Feedback Techniques

What is Feedback? What is Feedback in Amplifier?

Feedback:

Feedback is a phenomenon of universal importance and has, therefore, entered the general vocabulary. Thus, consider the following situation: you are an officer. You have instructed a subordinate to do a certain job. After some time, the person informs you about the state of job, whether satisfactorily completed or there are some difficulties. Thus, information constitutes the feedback. You definitely want this feedback to ensure that the job was been done; if not then what corrective measures are to be adopted.

Feedback in Amplifier:

Feedback is the process of picking up a part of the output signal of an amplifier and feeding it at the input.

The voltage so fed back to the input is called the feedback voltage.

Voltage Feedback: In voltage feedback, the feedback voltage is proportional to the output voltage.

Current Feedback: In current feedback, the feedback voltage is proportional to the output current.

Positive Feedback: Feedback is called positive (or regenerative) feedback, when the feedback signal is in phase with the input and adds to the input signal. This results in increase of the gain of the amplifier. But it has the disadvantage of increased instability of gain, increased distortion and noise. Hence, positive feedback is rarely used in amplifiers. However positive feedback is used in oscillators.

Negative (Inverse) Feedback: Feedback is called negative, inverse or degenerative when the feedback signal is out of phase with the input signal and subtracts from it. this results in reduction in the gain of the amplifier.

History of Negative Feedback: H.S. black in 1928 introduction the concept of negative feedback in amplifiers but was ridiculed since negative feedback reduces the gain of an amplifier. But today negative feedback is used in all good quality amplifiers because of its several merits.

Merits of Negative Feedback

Increased stability of gain.
Reduction in distortion and nonlinearity.
Flat response over a wider frequency range.
Reduction in noise generated within the amplifier.
Desired change in output and input impedances.

As more and more negative feedback is used, the characteristic of feedback amplifier become less and less dependent on the characteristics of the open loop (xero feedback) amplifier and ultimately depend on thee properties of the feedback network itself. In fact, operational amplifiers (OP Amp) are usually used in the high loop gain limit with extremely large open loop voltage gain, exceeding a million.

Feedback Techniques | Feedback in Amplifier

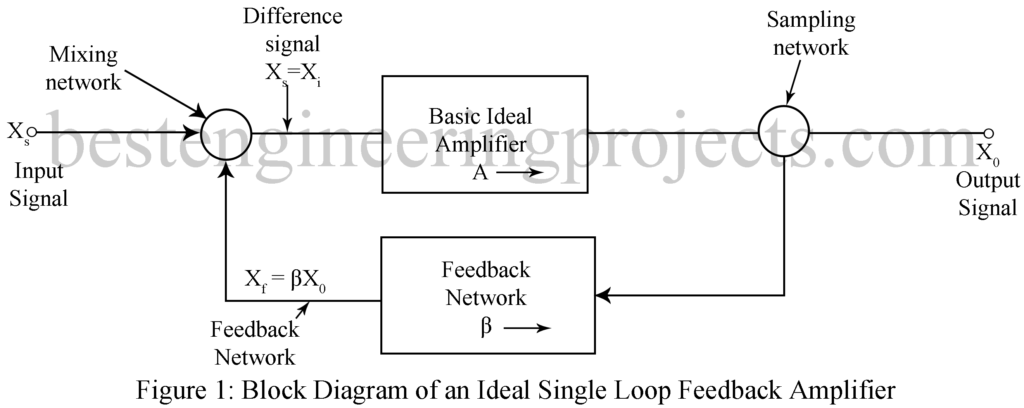
Figure 1 gives the block diagram of a single loop feedback amplifier. The functions of different constituent parts are as under.

Basic Ideal Amplifier: This provide gain A to the signal X_i fed to it.

Sampling Network: It samples the output signal X₀ and applies this signal to the feedback network. Sampling may be of two types: (a) Voltage sampling and (b) Current sampling shown respectively in figure 2 and figure 3. In voltage sampling method shown in figure 2, the feedback network is connected in shunt with the output voltage V₀. Figure 3 shows the method of sampling the output current. Here the feedback network appears in series with the load impedance.

Feedback network: The feedback network is generally in the form of passive two port network and may be formed of resistor, capacitors, and inductors. In most cases, however, the feedback network uses only resistors.

Mixing Network: The voltage at the output of feedback network is mixed with the signal voltage in one of the following two ways: (i) series mixing as shown in figure 4 and (ii) shunt mixing as shown in figure 5.

Gain with Feedback | Feedback in Amplifier

In figure 1, A represents the gain of the internal amplifier without feedback. Further X_s, X_o, X_f and X_d represent respectively the input signal, output signal, feedback signal and difference signal. Each of these signals may represent either a voltage or a current.

The difference signal or the error signal X_d equals the input signal minus the feedback signal. Thus,

$X_d = X_s-X_f$ ………(i)

The reverse transmission factor of the feedback network denoted by $\beta$ is defined as,

$\beta = \dfrac{X_f}{X_0}$ ……..(ii)

Generally, the reverse transmission factor $\beta$ is real number but, in a general case, it may be a complex function of the frequency of the input signal.

In an ideal amplifier, the output signal is proportional to the input and this factor of proportionality is independent of the magnitude of the source impedance R_s and the load impedance R_L.

Thus, $X_o = A\times X_i = A\times X_d$ …..(iii)

On combining Equations (i), (ii) and (iii) we get,

$X_0 = A \times (X_s-X_f) = A\times (X_s-\beta X_o)$ …….(iv)

Or, $X_o \times (1 + A \beta) = A \times X_s$

Let A_f be the gain of the amplifier with feedback.

Then, $A_f = \dfrac{X_o}{X_s} = \dfrac{A}{1 + A \beta}$ ……(V)

Equation (V) is called feedback equation.

If |A_f| < |A| i.e. when the gain has reduced due to feedback, the feedback is negative, inverse or degenerative. This condition occurs when $|1 + A\beta|$ exceeds unity. On the other hand, if |A_f| > |A| i.e. when the gain has increased due to feedback, the feedback is positive or regenerative.

Loop Gain | Feedback in Amplifier

Figure 1 shows that the difference signal X_d (i) gets multiplied by A in passing through the basic amplifier (ii) gets multiplied by $\beta$ in passing through the feedback network and (iii) is multiplied by -1 in the mixing network. In this complete process, the signal has traveled from the input terminals of the basic amplifier around the loop formed by the basic amplifier, feedback network and the mixing network and gets multiplied by the factor $-A\beta$ . The quantity $-A\beta$ is called the loop gain, return ratio or the loop transmission feedback factor.

Numerical Example Regarding Feedback in Amplifier

Examples: 1 A feedback amplifier has voltage gain of -1200 without feedback. If feedback with feedback factor $\beta = -0.1$ is introduced in the circuit, calculate the voltage gain with feedback.

Solution: $A = -1200$

$\beta =-0.01$ Hence voltage gain with feedback is,

$A_f = \dfrac{A}{1+A\beta} = \dfrac{-1200}{1+(-1200)(-0.1)} = \dfrac{-1200}{121} = -9.92$

Example 2: Voltage gain of an amplifier is +1000. On application of negative feedback, the gain reduced to +100. Find the feedback factor $\beta$

Solution: $A = 1000$

$A_f = 100$ $A_f = \dfrac{A}{1+A\beta}$

Hence, $100 = \dfrac{1000}{1 + 1000\beta}$

Or, $100 + 10,000\beta = 1000$

Hence, $\beta = \dfrac{1000-100}{10,000} = 0.09$

Example 3: On application of negative feedback to an amplifier of voltage 200, the overall gains falls to 100 (i) Calculate the feedback factor $\beta$ . (ii) With $\beta$ maintained constant, calculate the value of voltage gain of basic amplifier A required to get a gain of 160 with feedback.

Solution: (i) $A = 200; \ A_f = 100$

$A_f = \dfrac{A}{1 + A\beta}$

Hence, $100 = \dfrac{200}{1 + 100\beta}$

Or, $100 + 20,000\beta = 200$

Hence, $\beta = \dfrac{100}{20,000} = 0.005$

(ii) $A_f = 160; \ \beta = 0.005$

Hence, $160 = \dfrac{A}{1+ 0.005 A}$

Or, $160 + 0.8 A = A$

Hence, $A = \dfrac{160}{1-0.8} = 800$

Example 4: Voltage gain of an amplifier without feedback is 100 and it reduces to 50 with negative feedback. Due to ageing process, let the gain without feedback falls to 80. Calculate the percentage reduction in voltage gain (i) without feedback and (ii) with feedback.

Solution: $A_f = \dfrac{A}{1+A\beta}$ Substituting the value,

$50 = \dfrac{100}{1 + 100\beta}$

Hence $\beta = 0.01$

(i) Without Feedback:

A = 100. It falls to 80 due to ageing

Hence percentage reduction is voltage gain $= \dfrac{100-80}{100}\times 100 = 20%$

(ii) With Feedback

The gain without feedback has fallen to 80

Hence with feedback $A_f = \dfrac{A}{1+A\beta} = \dfrac{80}{1+ (80\times 0.01)} = 44.44$

Hence, the percentage reduction in gain $= \dfrac{50-44.44}{50}\times 100 = 11.12%$