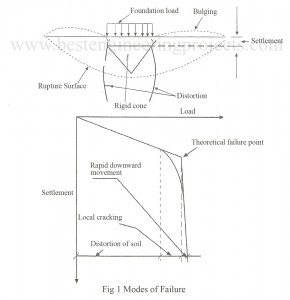
What are the types of shear failure? According to Vesic (1973) there are three types of shear failures. They are: General Shear failure Local Shear failure Punching Shear failure These failures are illustrated in Fig 1, 2 and 3. General Shear Failure – This type of failure occurs in stiff clay or dense sand. In this type of failure, failure takes place at a very small strain. The load settlement curve shows a well-defined peak as shown in Fig.1. At failure entire soil mass within the failure wedge participates and well…
Read MoreCategory: Civil Projects
Bearing Capacity Theories
Bearing Capacity Theories: When a footing is placed on a soil, the soil deforms and foundation settles as shown in the figure 1. Before failure takes place, the soil below the foundation undergoes into various stages. At first the soil gets distorted. Local cracking follows this after which a rigid cone of the soil is formed directly below the footing. Lastly rupture surfaces are developed and failure of the soil occurs along these rupture surfaces. The stages of failure of bearing capacity theories foundation soil are briefly described below. Distortion…
Read MoreStability Analysis for Cantilever Wall
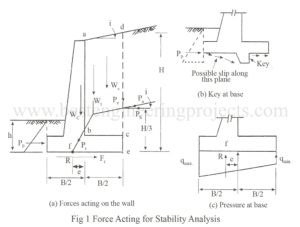
Derivation of Stability Analysis for Cantilever Wall Consider a cantilever wall carrying a sloping backfill as shown in the Fig.1. The various forces acting on the wall are: Pa = Active earth pressure acting at a height H/3 from the base on section ed. Ph = Pa cosi Pv = Pa sini Ws = Weight of soil abcd Wc = weight of wall including base Wt = the resultant of Ws and Wc Pt = the resultant of Wt and Pa meeting at f at base of Wall Pp =…
Read MoreStability of Different Type of Retaining Walls
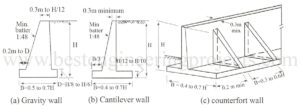
What is the Stability of Different Types of Retaining Walls? Figure 1 shows gravity, cantilever, and counterfort types of retaining walls. The stability of a gravity wall is due to the self-weight of the wall and the passive resistance developed in front of the wall. The gravity walls are designed using Coulomb’s theory. Reinforced concrete walls (cantilever or counter-fort types) are more economical than gravity walls because the backfill itself provides most of the required dead load. Rankine’s theory is used to investigate the stability of reinforced concrete walls. The…
Read MoreCulmann Graphical Method for Active and Passive Case
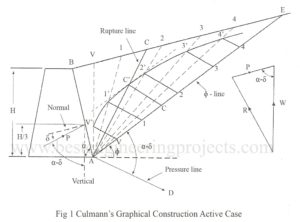
Culmann Graphical Method for Active and Passive Case: In this method a retaining Wall is drawn to a suitable scale as shown in the Fig.1 below. The Various steps in the procedure are: Draw [late] \phi [/latex]-line AE at an angle with the horizontal. Lay off on AE distances AV, A1, A2, A3 etc to a suitable scale to represent the weight of wedges ABV, AB1, AB2, AB3, and so on. Lay off AD at an angle equal to to the line AE. The line AD is called pressure line.…
Read MoreCoulomb derivation based on limit equilibrium approach for Passive Case
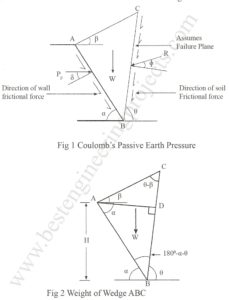
Figure 1 below shows the cross section of a retaining wall. Weight of Wedge ABC From Triangle ABC, Area of Triangle ABC = Therefore: – Again, Area of Triangle of Forces for W, Pp and R From the sine rule, Substituting the value of W from the equation (3.34) into (3.35) we get, In order to get the maximum value of Pp, Where, Note: When, (leveled backfilled), (no wall friction) and (vertical interface between wall and backfill), then, . The point of application of Pp is at a…
Read MoreCoulomb’s Wedge Theory | Derivation for Active Case
Coulomb’s made the following assumptions in the development of his theory and hence it is called Coulomb’s Wedge Theory. The assumptions made by Coulomb while giving his theory was: The soil is isotropic and homogeneous. The surface of rupture is a plane. The failure wedge is a rigid body. There is friction between and the wall. Back of wall need not be vertical. Failure is two dimensional. The soil is cohesion-less. Coulomb’s equation of shear strength is valid. Coulomb made his derivation based on limit equilibrium approach. Derivation of Active…
Read MoreDerivation of Equation by Trial Wedge Method for Passive Case
In this article we will discuss about derivation of equation by trial wedge method for passive case. The equation is derived as follows. A planar failure wedge IJM is considered. There are distributed normal stresses along IJ and JM and distributed along JM. The resultants of these stresses are carried out in the analysis. In this case, the force F acts above the normal and the angle between the force F and weight W will be . The forces acting at the free body IJM are: Weight of wedge =…
Read MoreDerivation of Equation by Trial Wedge Method for Active Case
Derivation of Equation by Trial Wedge Method for Active Case: Figure 1 below shows the application of the trial Wedge method to the problem of simple retaining wall without wall friction. A planar failure wedge IJM is considered. There are distributed normal stresses along IJ and JM and distributed shear stress along JM. The resultants of these stresses are carried out in the analysis. The forces acting at the free body IJM are: let’s start the derivation of equation by trial wedge method Weight of wedge = Pa…
Read MoreTrial Wedge Method
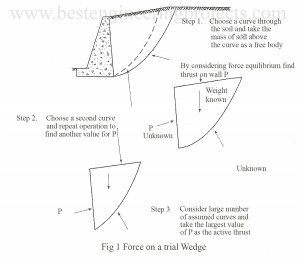
The trial wedge method of analysis is shown in Fig.1 below. The following steps are to be followed to make the analysis. Step 1 – a mass of soil behind the wail is considered as a free body. The force P, which must exist between the free body and the wall, is found by writing the equation of equilibrium for the free body as a whole. Step 2 – a different free body is considered, having a different boundary through the soil. Once again the required force between the…
Read More