Volt Ampere Characteristic of a PN Diode

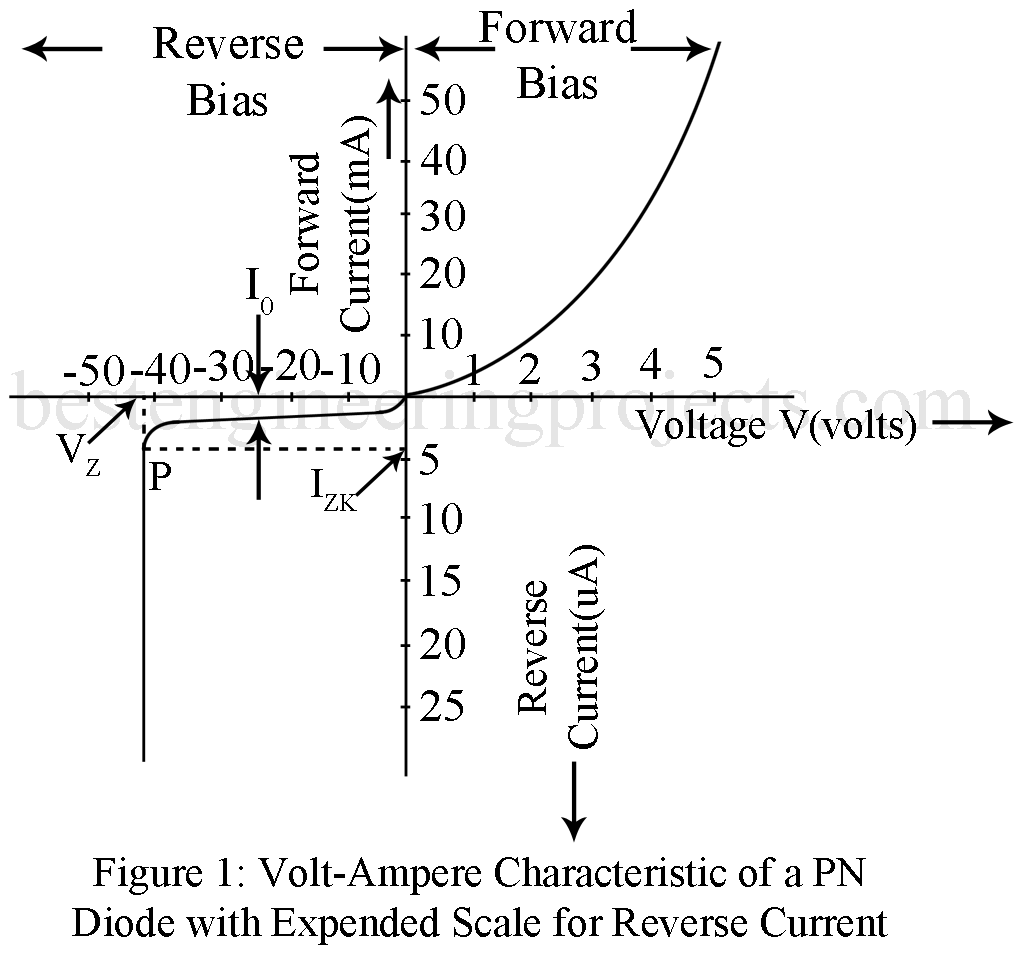
What is Volt Ampere Characteristic of PN Diode?

Current I in a PN diode in related to the junction voltage V_V by the relation given by equation,

$I = I_0 [e^{\dfrac{V}{\eta V_T}}-1]$ ………..(1)

Figure 1 gives the typical volt-ampere characteristic for a PN diode plotting above equation. With forward bias, the forward current remains essentially zero until the so called Cutin voltage V_V of t diode is reached. This cutin voltage is defined as the voltage below which the forward current is less than 1% of the maximum rated current of the diode. This cutin voltage is also known as the turn-on voltage or threshold voltage. The cutin voltage varies with the semiconductor material and with the method of fabrication. Typically, the cutin voltage is about 0.2 volt for Ge diode and about 0.6 volt for Si diode. This higher value of cutin voltage in Si diode results mainly due to low value of I_O.

From figure 1 we observe that beyond the cutin voltage, the forward current increases rapidly with the increase of forward voltage. In the range of forward voltage, the applied voltage is much larger than V_T (0.026 volt at 300 K) so that in above equation we may neglect 1 in comparison with $e^{\dfrac{V}{\eta V_T}}$ and reduced to the following simpler form

$I = I_0 e^{\dfrac{V}{\eta V_T}}$ ………(2)

With small reverse bias, the reverse current increases with increases with increase in the magnitude of reverse bias. When the reverse bias magnitude exceeds several times V_T, we may neglect $e^{\dfrac{V}{\eta V_T}}$ is comparison with I and the reverse current becomes steady at value I_O. with further increase of reverse voltage, the breakdown takes place and the reverse current then increases abruptly at an almost constant value of reverse voltage V_Z.

Temperature Dependent of Volt Ampere Characteristic

Total Reverse Saturation Current:

Total or measured value of reverse saturation current $I_{ot} = (I_0 + I_R)$ where I₀ is the theoretical value of reverse saturation current and I_R is the leakage reverse current component. I_R is independent of temperature whereas I₀ is heavily dependent on temperature.

$I_0 = Aq[\dfrac{D_p}{L_pN_D} + \dfrac{D_n}{L_nN_A}]n_i^2$ …….(3)

This equation gives I₀ as a function of D_n, D_p and n_i². But n_i² depends on temperature as given by equation below

$n_i^2 = A_O T^3 \epsilon^{\dfrac{-E_{GO}}{k_T}}$ ……..(4)

Voltage V_T is also proportional to temperature T. Further D_p and D_n depend on temperature T. Accordingly a general expression for I₀ valid for both Ge and Si diodes is,

$I_0 = k T^m e^{-\dfrac{V_{G0}}{\eta V_T}}$ ……….(5)

Where k is a constant, m is a constant for the material, qV_G0 is the forbidden energy gap in joules. Experimentally it is found that reverse saturation current $I_{ot} = (I_0 + I_R)$ increases at the rate of 7% per deg C for both Ge and Si diodes. But $1.07^{10} \approx 2.0$ . Hence, we conclude that the total reverse saturation current doubles for every 10⁰ C rise in temperature.

Cutin Voltage:

The following relation is found valid for both Ge and Si diodes,

$\dfrac{dV}{dT} = -2.5 \dfrac{mV}{deg C}$ ……..(6)

Thus, V and also V_V decrease with the increase of temperature at the rate of 2.5 mV/deg C. Although the cutin voltage V_V and total reverse saturation current change with temperature, the shape of the overall V-I characteristic of diode does not change with temperature.

Diode resistance:

Static Diode Resistance R

It is the ratio of diode voltage to diode current. It varies greatly as the operation point shifts. It does not form a useful parameter of diode.

Dynamic or Incremental Diode Resistance r

It is defined as,

$r = \dfrac{dV}{dI}$ ……….(7)

Thus, dynamic resistance of a diode is the reciprocal of the slope of current versus voltage characteristic and forms an important device parameter for small signal operation. However, the dynamic diode resistance r varies with the operation point.

From, equation (1),

$r = \dfrac{dV}{dI} = \dfrac{\eta V_T}{I_0 e^{\dfrac{V}{\eta V_T}}} = \dfrac{\eta V_T}{1 + I_0}$ ……..(8)

For reverse bias greater than a few tenth of a volt, $|\dfrac{V}{\eta V_T}|>>1$ and negative. Hence, $e^{\dfrac{V}{V_T}}$ is extremely small composed to unity and hence r is extremely large.

For forward bias greater than a few tenth of a volt,

$|\dfrac{V}{\eta V_T}|>1$ and as per equation (1), I>>I₀. Then from Equation (8).

$r \approx \dfrac{\eta V_T}{I}$ ………(9)

Equation (9) shows that for forward bias, r various inversely with the current I.

At room temperature (300 K), V_T = 0.026 volt. Then for $\eta = 1$ ,

$r(ohms) = \dfrac{26}{I(mA)}$ …….(10)

Thus, for $I = 26 mA, r = 1\Omega$

Example 1: An ideal Ge diode operating at temperature of 100⁰C, has reverse saturation current $I_0 = 20 \mu A$ . At 100⁰C, find the dynamic resistance of the diode for a bias of 0.1 volt (a) in the forward direction and (b) in the reverse direction.

Solution:

At 100⁰C, T = 273 + 100 = 373⁰K,

Hence, $V_T = \dfrac{373}{11600} = 0.0321 volt$

For Ge, $\eta = 1$

Hence, $I = I_0(e^{\dfrac{V}{V_T}}-1)$

Now, $g = \dfrac{1}{r} = \dfrac{dI}{dV} = \dfrac{I_{0(100)} e^{\dfrac{V}{V_T}}}{V_T}$

For forward bias of 0.1 volt,

Hence, $r = \dfrac{1}{g} = \dfrac{1}{0.014} = 71.4 \Omega$

For reverse bias of 0.1 volt,

$g = \dfrac{20 \times 10^{-6}}{0.0321}e^{\dfrac{-0.1}{0.0321}} = 24.9 \times 10^{-6}S$

Hence, $r = \dfrac{10^6}{24.9}\Omega = 36 k\Omega$

Piecewise Linear Approximation of Diode Characteristic

For large single operation, it is usually sufficient to use a piecewise linear representation of the V-I characteristic of PN diode. Figure 2 shows a piecewise linear approximation. For V < V_V the current rises with a constant slope. In this region, the diode has a constant incremental resistance $r = \dfrac{dI}{dV}$ . In this forward bias region, this resistance r is designated as R_f and is called the forward resistance.