Influence of Water table on Bearing Capacity

Terzaghi has developed the bearing capacity equation on the assumption that water table is at great depths. If water table is present close to the foundation, some modification is necessary. This is done as per the followings.

Case 1 Water table above footing base

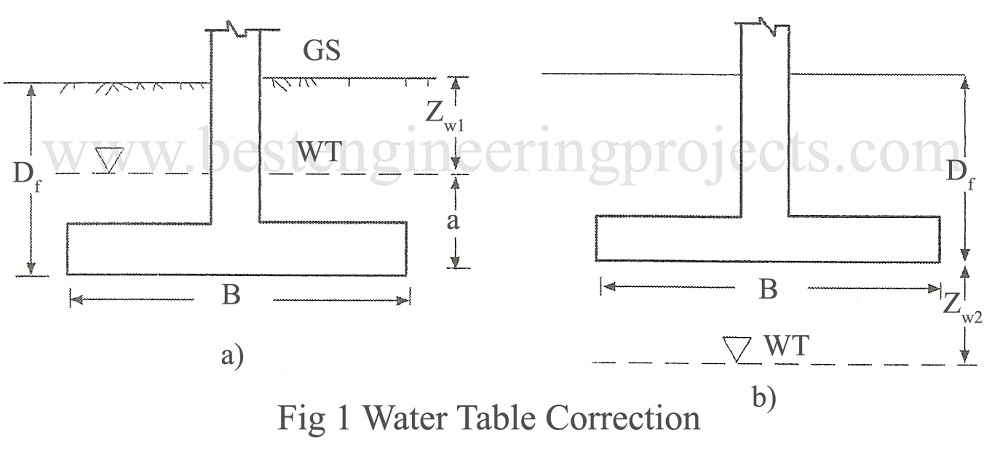
The weight of soil below water table is reduced due to buoyancy. The influence of water table on bearing capacity is incorporated in the general bearing capacity equation with the help of Fig.1.

Let,

Z_w1 = Depth of water table below ground level

a = Height of water table above base of the footing

D_f = Depth of foundation.

B = Width of foundation

$\gamma_{sub}$ = Submerged unit weight of soil

$\gamma$ = Soil unit weight

R_W1 = Correction factor for depth term

R_W2 = Correction factor for width term

If the water table is at a depth Z_W1 such that 0 < Z_W1 < D_f then, the bearing capacity equation is written as:

$Q_{ult} = cN_c + [\gamma Z_{w1} + (D_f-Z_{w1})\gamma_{sub}]N_q + \dfrac{1}{2}\gamma_{sub} BN_{\gamma}$

$Q_{ult} = cN_c + \gamma D_f N_q R_{w1} + \dfrac{1}{2}\gamma_{sub} BN_{\gamma}$ ———- (1)

Where R_W1 can be obtained from:

$[\gamma D_w + (D_f-Z_{w1})\gamma_{sub}] = \gamma D_f R_{w1}$

$\dfrac{\gamma Z_{w1} + (D_f-Z_{w1})\gamma_{sub}}{\gamma} = D_fR_{w1}$

$Z_{w1} + \dfrac{1}{2}(D_f-Z_{w1}) = D_fE_{w1}$

$\dfrac{1}{2}Z_{w1} + \dfrac{1}{2}D_f = D_fR_{w1}$

$D_fR_{w1} = \dfrac{1}{2}Z_{w1} + \dfrac{1}{2}_f$

$R_{w1} = \dfrac{1}{2}\dfrac{Z_{w1}}{D_f}+\dfrac{1}{2}\dfrac{D_f}{D_f}$

$R_{w1} = \dfrac{1}{2}(1+ \dfrac{Z_{w1}}{D_f})$

R_W1 = ½ (1 + Z_W1/D_f) ———- (2)

Case 2 – Water table below footing base

In this case, soil above the base of the footing is moist and below base may be fully or partially submerged. If the water table is at the base then the bearing capacity equation is written as:

$Q_{ult} = cN_c + \gamma D_fN_q + \dfrac{1}{2}\gamma BN_{\gamma}R_{w2}$ ———- (3)

If the water table is at a depth B below the case of the footing then the bearing capacity is not affected and no correction is required. If the water table is at an intermediate depth say, Z_W2 below the base of the footing where 0<Z_W2<B, then the bearing capacity equation is Written as:

$Q_{ult} = cN_c + \gamma D_fN_q + [\dfrac{1}{2}z_{w2}\gamma + \gamma_{sub}(B-Z_{w2})]N_{/gamma}$

$Q_{ult} = cN_c + \gamma D_fB_q + \dfrac{1}{2}\gamma BN_{/gamma}E_{w2}$ ———- (4)

Where, R_W2 can be obtained from the equation:

$Z_{w2}\gamma + \gamma_{sub}(B-Z_{w2}) = B\gamma R_{w2}$

$Z_{w2} + \dfrac{\gamma_{sub}}{\gamma}(B-Z_w2) = BR_{w2}$

$Z_{w2} + \dfrac{1}{2}B-\dfrac{1}{2}Z_{w2} = BR_{w2} = BR_{w2}$

$\dfrac{1}{2}\times Z_{w2} + 0.5B = BR_{w2}$

$BR_{w2} = 0.5(Z_{w2} + B)$

$R_{w2} = 0.5(1 + \dfrac{Z_w2}{B})$ ———- (5)

When the water table at base, Z_W2 = 0 and R_W2 = 0.5 and when Z_W2 = B, R_W2 = 1. This means when water table is at base the weight term in the bearing capacity equation is reduced by half and when water table at great depth ( i.e. greater than width of foundation below the base of foundation) water table will have no influence in the bearing capacity.

2 Thoughts to “Influence of Water table on Bearing Capacity”

Yirga Mulaw

April 5, 2017 at 6:27 pm

Hiiiiiiiiiiiii sir;how you are I want ask you some foundation questions

Yirga Mulaw

April 5, 2017 at 6:32 pm

given ; bulkdensity=30KN/M CUBIC, dry density=28 , cohesion(c)=19, internal friction=24degree then calculate ultmate bearing capacity of for mat foundation ok only the formula

Share this:

2 Thoughts to “Influence of Water table on Bearing Capacity”

Leave a Comment Cancel reply