Design of Pile Foundation | Efficiency of Pile Groups

Engineeering Projects

The spacing of the piles is usually predetermined by practical and economical considerations. The design of a pile foundation is usually comprises:

  1. Determination of the ultimate load bearing capacity of the group Qu(g)
  2. Determination of settlement of the group s(g)

It is well known that the ultimate load of the group is generally different from the sum of the ultimate loads of individual piles Qu(s).

E_f = \dfrac{Q_u(g)}{nQ_u(s)}\times 100% ——— (1)

Where, Ef = Group efficiency ratio

Qu(g) = Ultimate bearing capacity of the pile group

Qu(s) = Ultimate bearing capacity of single pile

The group efficiency depends on the type of soil, method of installation, spacing, load per pile and numbers of pile in the group.

There is no acceptable “efficiency formula” for group bearing capacity. There are few formulas such as FLED rule, Converse Labare Formula that are sometimes used by engineers. These formulas are empirical and give efficiency less than unity. But when piles are installed in sands efficiency factor can be greater than unity as shown by Vesic. There is not much experimental evidence to determine the group efficiency for piles embedded in clay soils.

There are many pile group efficiency equations. These equations are to be used cautiously. In many cases, they are no better than a good guess. The Converse Labare Formula is one of the most widely used formula and is expressed as:

E_g = 1-\theta{\dfrac{(n-1)m + (m-1)n}{90mn}}   ———- (2)

Where, m = number of rows in a group

n = number of piles in a rows

\theta = tan^{-1}(\dfrac{d}{s})

d = diameter of the piles

s = spacing of the piles

As per Tomlinson, when spacing of piles in a group is twice the pile diameter, the efficiency is about 0.7. When it is increased to 8 diameters, the efficiency reaches to unity. Thus we can write,

Q_u(g) = \eta[nQ_u(s)]   ———- (3)

Where, \eta is the efficiency of the group and n is the number of piles in the group.

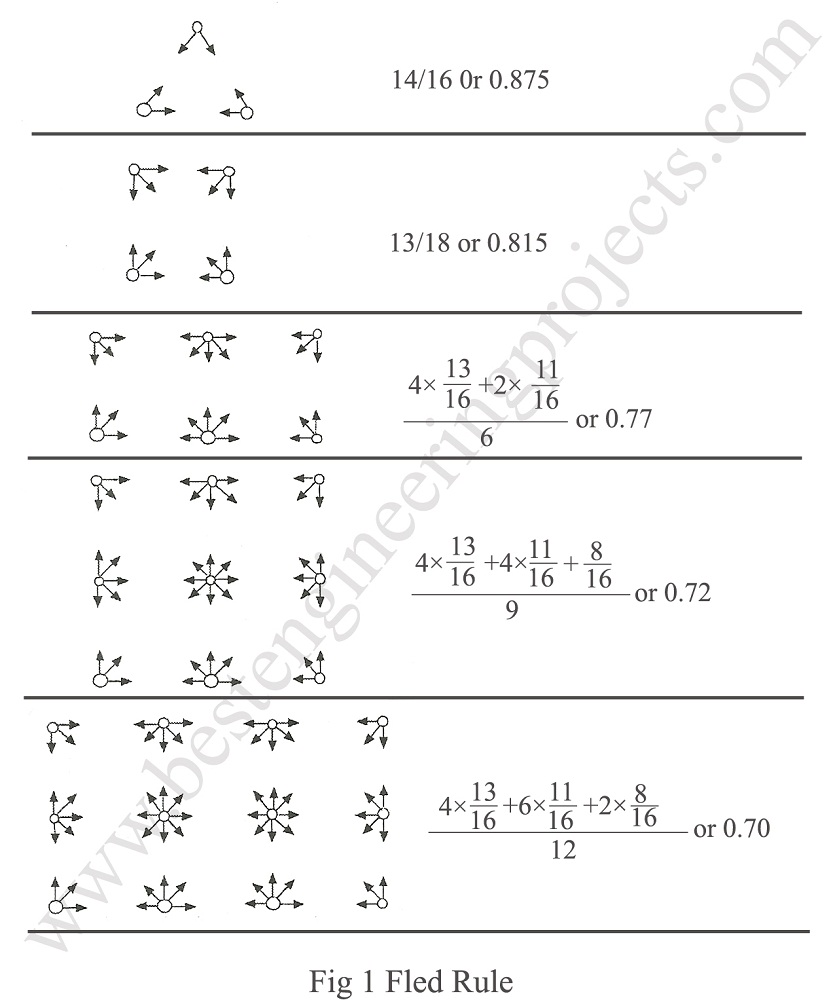
FLED’S RULE – As per the rule recommended by Fled the capacity of pile is decreased by 1/16 for each adjacent pile.

fled rule

The computation of efficiency for various pile groups is shown in Fig.1 above.

Leave a Comment