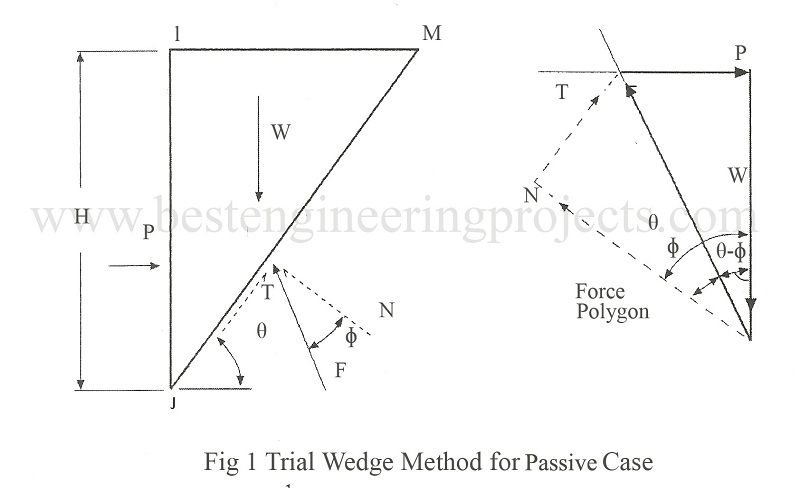
Derivation of Equation by Trial Wedge Method for Passive Case

In this article we will discuss about derivation of equation by trial wedge method for passive case. The equation is derived as follows. A planar failure wedge IJM is considered. There are distributed normal stresses along IJ and JM and distributed along JM. The resultants of these stresses are carried out in the analysis. In this case, the force F acts above the normal and the angle between the force F and weight W will be $\theta + \phi$ .

The forces acting at the free body IJM are:

Weight of wedge = $\dfrac{1}{2}\times Area\ IJM \times \gamma$

$= \dfrac{1}{2}\times IM\ IJ \times \gamma$

$= \dfrac{1}{2}\times Hcot\theta \times H \times \gamma$

$= \dfrac{1}{2}\gamma H^2 cot \theta$

P_p = resultant of distributed stress between soil and wall

N = resultant of normal stresses within soil along assumed plane wall

T = resultant of shear stresses within soil along assumed plane wall

= N tan $\phi$

Considering the equilibrium of the wedge and referring the force polygon we have,

$P_P = \dfrac{1}{2} \gamma H^2 cot\theta \times Tan(\theta + \phi)$ ……….(1)

Now the problem is to find out the maximum value of P to fail the wedge in the active case. This is done by differentiating P_p with respect to $\theta$ and equating to Zero. Then:

$\dfrac{\partial P_P}{\partial \theta} = 0$

$\dfrac{\partial P_P}{\partial \theta} = \dfrac{1}{2}\gamma H^2[\dfrac{-Tan(\theta + \phi)}{sin^2\theta} + \dfrac{cot\theta}{cos^2(\theta + \phi)}] = 0$