Coulomb's Wedge Theory | Derivation for Active Case

Coulomb’s made the following assumptions in the development of his theory and hence it is called Coulomb’s Wedge Theory.

The assumptions made by Coulomb while giving his theory was:

The soil is isotropic and homogeneous.
The surface of rupture is a plane.
The failure wedge is a rigid body.
There is friction between and the wall.
Back of wall need not be vertical.
Failure is two dimensional.
The soil is cohesion-less.
Coulomb’s equation of shear strength is valid.

Coulomb made his derivation based on limit equilibrium approach.

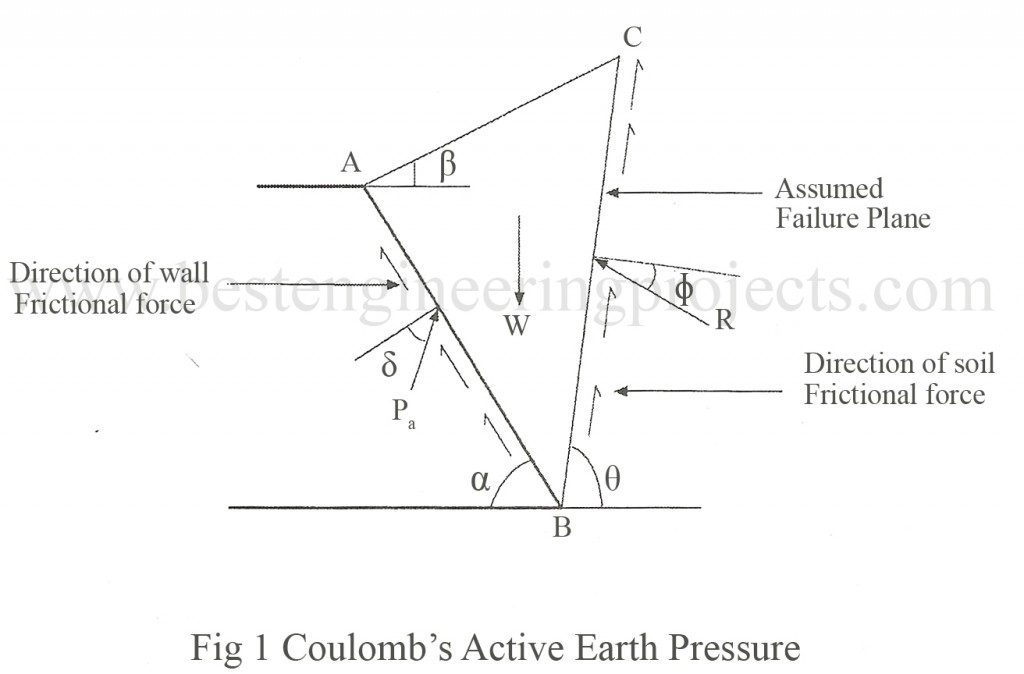
Derivation of Active Case for Coulomb’s Wedge Theory

Figure 1 below shows the cross section of a retaining Wall. Equilibrium analysis of failure wedge ABC involves:

Weight of wedge ABC (magnitude and direction known)
P_a (direction known, magnitude unknown)
R (direction known, magnitude unknown)

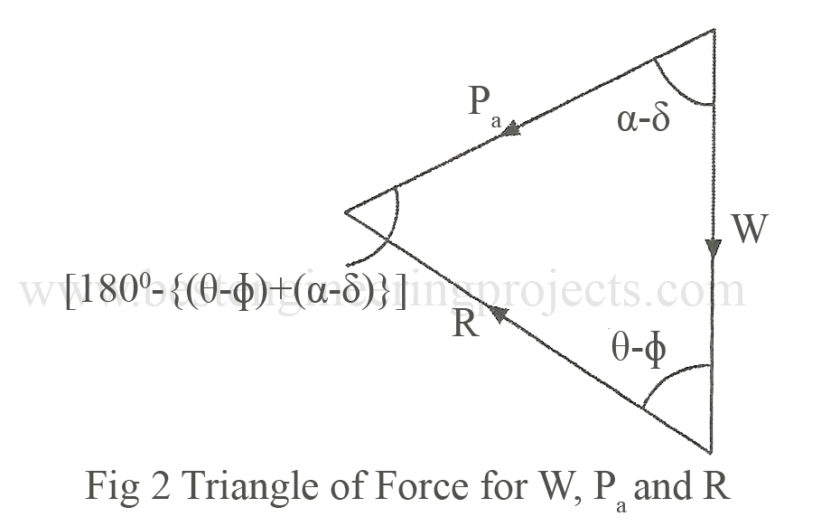
Hence, from the triangle of forces can be drawn and P_a can be determined.

Calculation of Weight of wedge ABC

From Triangle ABC,

Area of Triangle ABC = $\dfrac{1}{2}AD\times BC$

$\dfrac{BC}{AB} = \dfrac{sin(\alpha + \beta)}{sin(\theta-\beta)}$

Therefore, $BC = AB\dfrac{sin(\alpha + \beta)}{sin(\theta-\beta)}$

Again, $AD = ABsin[180^0-(\alpha+\theta)] = ABsin(\alpha + \theta)$

$Area \ of\ \Delta ABC = \dfrac{1}{2}AB\ sin(\alpha + \theta) \times AB \dfrac{sin(\alpha + \beta)}{sin(\theta-\beta)}$

$\Delta ABC = \dfrac{H^2}{2sin^2a}[sin(\alpha + \theta) \dfrac{sin(\alpha + \beta)}{sin(\theta-\beta)}]$

$W = \gamma \times V = \dfrac{\gamma H^2}{2sin^2a}[sin(\alpha + \theta) \dfrac{sin(\alpha + \beta)}{sin(\theta-\beta)}]$ …….(1)

Triangle of Forces for W, P_a and R | Coulomb’s Wedge Theory

From the sine rule we can write,

$\dfrac{P_a}{sin(\theta-\phi)} = \dfrac{W}{sin[180^0-((\theta-\phi)+(\alpha-delta))]}$ ……..(2)

Substituting the value of W from the equation (1) into (2) we get,

$P_a = \dfrac{\gamma H^2}{2sin^2\alpha}[sin(\alpha + \theta) \dfrac{sin(\alpha + \beta)}{sin(\theta -\beta)}] \dfrac{sin(\theta -\phi)}{sin(180^0 -\theta + \phi -\alpha + \delta)}$

In order to get the maximum value of P_a,

$\dfrac{\partial P_a}{\partial \theta} = 0$

$P_a = \dfrac{\gamma H^2}{2}[\dfrac{sin^2(\phi + \alpha)}{sin^2\alpha sin(\alpha -\delta(1 + \sqrt{\dfrac{sin(\phi + \delta) sin(\phi -\beta)}{sin(\alpha -\delta) sin(\alpha + \beta)}}))}]$

$P_a = K_a \dfrac{\gamma H^2}{2}$

Where,

$K_a = [\dfrac{sin^2(\phi + \alpha)}{sin^2\alpha sin(\alpha -\delta(1 + \sqrt{\dfrac{sin(\phi + \delta) sin(\phi -\beta)}{sin(\alpha -\delta) sin(\alpha + \beta)}}))}]$

Note:

When, $\beta = 0$ (leveled backfilled), $\delta = 0$ (no wall friction), then $K_a = \dfrac{1-sin\phi}{1+sin\phi}$ . The point of application of P_a is at a distance of H/3 above the base of the wall.