Analysis of Common Emitter Amplifier using h-parameters

Analysis of Common Emitter Amplifier using H Parameter

Figure 1(a) shows the circuit of a common emitter (CE) amplifier using self-bias and load resistor R₀ capacitively coupled to the collector. Figure 1(b) gives the a.c. equivalent circuit. Here we have eliminated the biasing circuit consisting of R₁, R₂, R_e, and C_z.

The R₁ – R₂ combination is equivalent to resistance R_b (= R₁ || R₂) between base and ground. It is assumed that R_b is large in comparison with the input resistance of the amplifier between base and ground and hence R_b is neglected in the equivalent circuit. Similarly, the reactance of capacitor C_z is so small at the lowest operating frequency that C_z effectively bypasses all a.c. components.

Hence R_e-C_z combination is also excluded from the a.c. equivalent circuit. In most of the amplifiers, the a.c. output voltage developed across R_c is capacitively coupled to the next stage through the capacitor C_b and R₀ is the effective impedance in the output circuit. The value of capacitor C_b is chosen so large that its reactance at the operating frequency is small and may be neglected. Then for a.c. the operation, R₀ comes in parallel with R_c, and effective load resistance R_L = R_C || R_O. This results in the simple a.c. equivalent circuit of Figure 1(b).

Analysis of Common Emitter Amplifier using H Parameter:

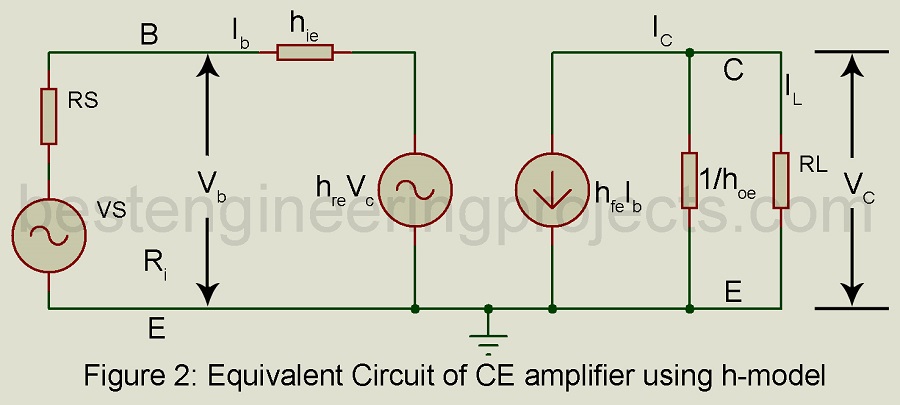
For analysis, we replace the transistor with its small-signal two generator h-parameter model. This results in the equivalent circuit of Figure 2. We assume sinusoidal input. Hence in the equivalent circuit of Figure 2, we have used the RMS value of voltages and currents namely I_b, V_b, I_c, and V_c.

Current Gain or Current Amplification:

Current gain is defined as the ratio of the load current I₁ to the input current I_b. Thus,

Current Gain $A_I = \dfrac{I_L}{I_b} = -\dfrac{I_c}{I_b}$ …..(1)

But from figure 2, $I_c = h_{fe}\times I_b + h_{oe}\times V_c$ …..(2)

Also $V_c = I_L\times R_L = -I_c\times R_L$ …..(3)

Combining Equation (2) and (3) we get,

$I_c = h_{fe}I_b-h_{oe}\times I_c \times R_L or (1+h_{oe}\times R_L)I_c = h_{fe}\times I_b$

Hence current gain $A_I = -\dfrac{I_c}{I_b} = -\dfrac{h_{fe}}{1+h_{oe}\times R_L}$ …..(4)

Input Impedance R_i:

This is the impedance between the input terminals B and E looking into the amplifier as shown in Figure 2 and is, therefore, given by,

$R_i = \dfrac{V_b}{I_b}$ ……(5)

From figure 2 $V_b = h_{ie}\times I_b + h_{re}\times V_c$ …..(6)

But $V_c = -I_c \times R_L = A_I I_b R_L$ …..(7)

Substituting the value of V_c from Equation (7) into Equation (6) we get,

$V_b = h_ie \times + h_{re} A_I I_b R_L$ …..(8)

Hence input impedance $R_i = \dfrac{V_b}{I_b} = h_{ie} + h_{re}A_IR_L$ …..(9)

$= h_{ie}-\dfrac{h_{fe}h_{re}}{h_{oe}+Y_L}$ …..(10)

Where $Y_L = \dfrac{1}{R_L}$

From Equation (10) we find that the input impedance R_i is also a function of load resistance R_L.

Voltage Gain or Voltage Amplification | Analysis of Common Emitter Amplifier using H Parameter:

It is the ratio of the output voltage V_c to the input voltage V_b. Thus,

Voltage Gain $A_v = \dfrac{V_c}{V_b} = -\dfrac{I_c R_L}{I_b R_i} = \dfrac{A_I R_L}{R_i}$ …..(11)

Output Admittance Y₀:

It is the ratio of the output current I_c to the output voltage V_c with V_s = 0. Hence

$Y_0 = \dfrac{I_c}{V_c}$ with V_S= 0 ……(12)

On substituting the value of I_c from Equation (2) into Equation (12) we get,

$Y_0 = h_{fe}\times \dfrac{I_b}{V_c} + h_{oe}$ …..(13)

But with V_s = 0, Figure 2 gives (R_s + h_ie) I_b+ h_re V_c = 0

Or $\dfrac{I_b}{V_c} = -\dfrac{h_{re}}{h_{ie}+R_s}$ ……(14)

Combining Equation (13) and (14) we get, $Y_0 = h_{oe}-\dfrac{h_{fe}\times h{re}}{h_{ie}+R_s}$ ……(15)

Equation (15) shows that the output admittance Y₀ is a function of source resistance R_s. If the source impedance is purely resistive, then the output impedance Y₀ is real i.e. purely conductive.

Output impedance $R_0 = \dfrac{1}{Y_0}$ …..(16)

In the calculation of Y₀, R_Lhas been considered external to the amplifier. If we include R_L in parallel with R₀, we get the output terminal impedance Z_t given by,

$Z<sub>t</sub> = \dfrac{R_0R_L}{R_0 + R_L}$ …..(17)

Overall Voltage Gain Considering R_s:

Source voltage V_s applied at the input of an amplifier results in voltage V_b between bae and emitter terminals (input terminals) of the transistor and voltage V_c at the output. Then the overall voltage gain considering the source resistance is given by

$A_{VS} = \dfrac{V_c}{V_s} = \dfrac{V_c}{V_b}\times \dfrac{V_b}{V_s} = A_V = \dfrac{V_b}{V_s}$ ……(18)

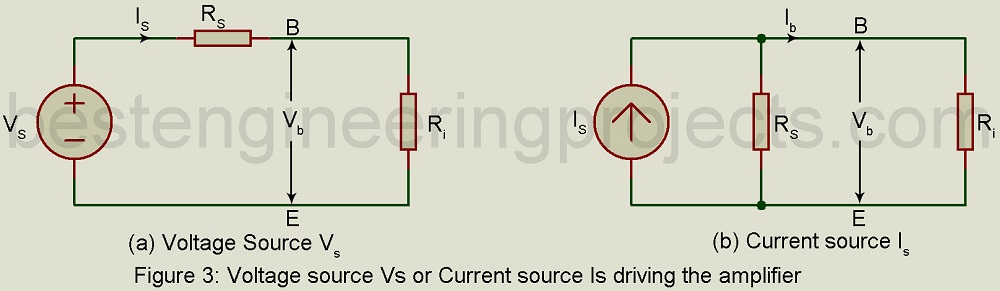
Figure 3(a) given the driven voltage source V_s with source resistance R_s in series. This form of an equivalent circuit for the energy source is known as Thevenin’s equivalent source. This energy source then drives the amplifier represented by its input resistance R_i.

Then $V_b = V_s\times \dfrac{R_i}{R_i+R_s}$ ……(19)

Hence overall voltage gain $A_{VS} = A_v \times \dfrac{R_i}{R_i + R_s}$ …..(20)

If R_s = 0, then A_VS = A_V. Thus, A_V forms a special care of A_VS with R_s = 0.

Overall Current Gain Considering R_s:

We may replace the voltage source V_s with series source resistance R_s by what is known as Norton’s equivalent source shown in Figure 3(b), consisting of current source I_s with source resistance R_s in the shunt. This current source drives the amplifier resulting in I_b at the input terminals of the amplifier and current I_L through the load impedance. Then the overall current gain A_Is is given by:

$A_{Is} = \dfrac{I_L}{I_s} = \dfrac{-I_C}{I_b}\times \dfrac{I_b}{I_s} = A_I\times \dfrac{I_b}{I_s}$ …..(21)

From Figure 3(b), $I_b = I_s\dfrac{R_s}{R_s+R_i}$ …..(22)

Hence overall current gain $A_{IS} = A_I \dfrac{R_s}{R_s + R_i}$ …..(23)

From Equations (20) and Equation (23) we get, $A_{VS} = A_{IS}\times \dfrac{R_i}{R_s}$ …..(24)

Equation (24) is true provided that the voltage source V_s and the current source I_s have the same source resistance R_s.

Power Gain A_p:

From the circuit of Figure 2, the average power delivered to the load imprudence R_L is given by:

$P_L = |V_C||I_C cos \theta|$ ……..(25)

Where $\theta$ is the phase angle between V_C and I_L. ……(26)

If load impedance is purely resistive, then cos $\theta = 1$ and Equation (26) reduce to:

$P_L = V_C \times I_L = -V_C \times I_C$ …..(27)

The input power at input port is, $P_i = V_b \times I_b$ …..(28)

The power gain A_P is the ratio of power P_L delivered to the load to the input power at the input port. Thus,

$A_P = \dfrac{P_L}{P_i} = \dfrac{-V_CI_C}{V_b \times I_b} = A_V \times A_I = A_I^2 \times \dfrac{R_L}{R_i}$ …..(29)

Table 1 gives the above derivations in tabular form. The expression for A_V, A_VS, and A_IS do not involve h-parameters, while the expression for A_I, R_i, and Y₀ involves the h-parameters. These expressions may be used for CB and CC configurations and also, of course, for using corresponding h-parameters.

Table 1: Result of small single analysis of low frequency ce amplifier
$A_I = -\dfrac{h_{fe}}{1+h_{oe}\times R_L}$	$A_V = \dfrac{A_I\times R_L}{R_i}$
$R_i = h_{ie} + h_{re}\times A_I \times R_L$	$A_{VS} \dfrac{A_{V}R_i}{R_i + R_s}$
$Y_0 = h_{oe}-\dfrac{h_{re}h_{fe}}{h_{ie}+R_s} = \dfrac{1}{Z_0}$	$A_{IS} = \dfrac{A_I R_s}{R_i + R_s}$