Stability Analysis for Cantilever Wall

Engineeering Projects

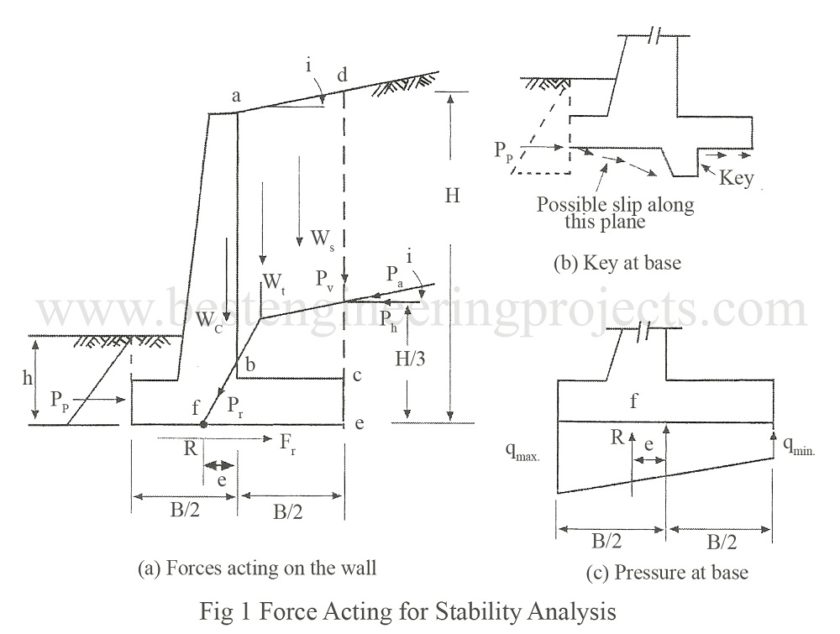
Derivation of Stability Analysis for Cantilever Wall

Consider a cantilever wall carrying a sloping backfill as shown in the Fig.1.

The various forces acting on the wall are:

Pa = Active earth pressure acting at a height H/3 from the base on section ed.

Ph = Pa cosi

Pv = Pa sini

Ws = Weight of soil abcd

Wc = weight of wall including base

Wt = the resultant of Ws and Wc

Pt = the resultant of Wt and Pa meeting at f at base of Wall

Pp = Passive earth pressure in front of the Wall

Fr = Base sliding resistance

e = eccentricity

Force Acting for Stability Analysis

Check against Sliding | Stability Analysis for Cantilever Wall

Force tending to slide the wall = Horizontal force due to back fill,

FD = Pa (h)

The force that resists the movement is:

F_r = c_aB + V tan\phi + P_P

Where, V = Ws + Wc + Pv

Ca = Unit adhesion between the wall and the soil at base

Factor of safety against sliding,

F_s = \dfrac{\Sigma F_r}{\Sigma F_D} = \dfrac{\Sigma F_r}{p_a(h)}\geq 1.5                  ………..(1)

In case, Fs < 1.5, additional factor of safety can be provided by providing one or two keys at the base as shown in Fig.1(b) above. In case the base is founded on soil of low bearing capacity and the wall happens to be very high, for such cases the only solution is to provide pile foundation to the wall. The passive earth pressure in front of the wall should not be relied upon unless it is certain that soil always remains firm and undisturbed.

Check against overturning | Stability Analysis for Cantilever Wall

For this, moment of all the resisting forces and stabilizing forces are taken about toe. The factor of safety against overturning is therefore:

F_0 = \dfrac{\Sigma M_r}{\Sigma M_0}\geq 2                ………(2)

Where, Mr = Resisting Moment

M0 = Overturning Moment

Check against Bearing Capacity Failure

If V is the resultant of all the vertical forces acting at f with an eccentricity e as shown in Fig.1(c). The pressure distribution at the base is trapezoidal with a maximum at toe and minimum at heel.

The intensity of pressure can be calculated by using the relation:

q_{max} = \dfrac{R}{B}[1 + \dfrac{6e}{B}]

and

q_{min} = \dfrac{R}{B}[1 - \dfrac{6e}{B}]           ……..(3)

The maximum pressure qmax cannot exceed the allowable bearing capacity of the soil. For no tension to develop at base the value of the eccentricity e should not exceed B/6. When, e = B/6, then qmin = 0. When e > B/6, qmin < 0 and tension will be developed and the heel of the wall gets lifted up. This situation should not be allowed to develop.

The depth of foundation provided should be adequate. It should be well below the zone of seasonal change in moisture and the frost. When the soil is of low bearing capacity and it is not practicable to provide large base slab it will be necessary to use a pile foundation to support the base slab which in turn supports the wall.

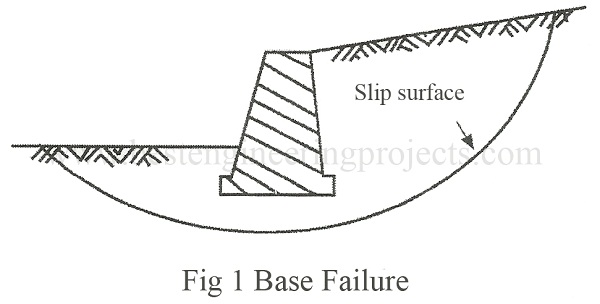
If the base of soil consists of medium to soft Clay, a circular slip circle may develop as shown in Fig.2. The critical slip surface must be located by trial. Such stability problems may be analyzed either by method of slices or any other methods such as friction circle method.

base failure

Leave a Comment