Instrumentation Amplifier | Derivation | Advantage

This article is all about instrumentation amplifier, its derivation, configuration, advantage and disadvantage. We had also try to describe different types of instrumentation amplifier like single op-amp based instrumentation amplifier, instrumentation amplifier using two and three op-amp.

The electrical transducer low level output signal often require to be amplified before further processing and this task is usually get accomplish by use of instrumentation amplifier.

There are several important characteristics of an instrumentation amplifier that set it apart from operational amplifier.

Instrumentation amplifier have finite gain which is selectable within precise value of range with high gain accuracy and gain linearity.
The instrumentation amplifier has a high impedance differential input.
The instrumentation amplifier has high common mode rejection ratio (CMMR) and a high common mode voltage range.
Instrumentation amplifier has high stability of gain with low temperature coefficient.

These listed out characteristics make an instrumentation amplifier superior to most OP-AMP.

Instrumentation Amplifier (IA) using one Op-amp

V_cm is external noise (common mode signal) and assuming internal resistance of source V₁ and V₂ are negligible and also assuming op-amp to be ideal.

$V^+ = \dfrac{R_4}{R_3 + R_4}(V_2 + V_{cm})$ …..(1)

Current through resistor R₁ = current through resistor R₂

$\dfrac{V_{cm}+V_1-V^+}{R_1} = \dfrac{V^+-V_0}{R_2}$ …..(2)

Combining equation (1) and (2) and eliminating V⁺, we get,

$V_0 = V{cm}\dfrac{R_4\times R_1-R_2\times R_3}{R_1\times (R_3 + R_4)}-\dfrac{R_2}{R_1}V_1 + \dfrac{R_4}{R_3}(\dfrac{1+\dfrac{R_2}{R_1}}{1+\dfrac{R_4}{R_3}})V_3$ …..(3)

Instrumental Amplifier shall reject common mode signal i.e. V₀ shall be independent of V_cm.

i.e. $V_{cm}\dfrac{R_4\times R_1-R_2\times R_3}{R_1\times (R_3 + R_4)} = 0$

$R_4\times R_1-R_2\times R_3=0$

$\dfrac{R_2}{R_1} = \dfrac{R_4}{R_3}$

The expression of output voltage from equation 3.

$V_0 = \dfrac{R_2}{R_1}(V_2-V_1)$

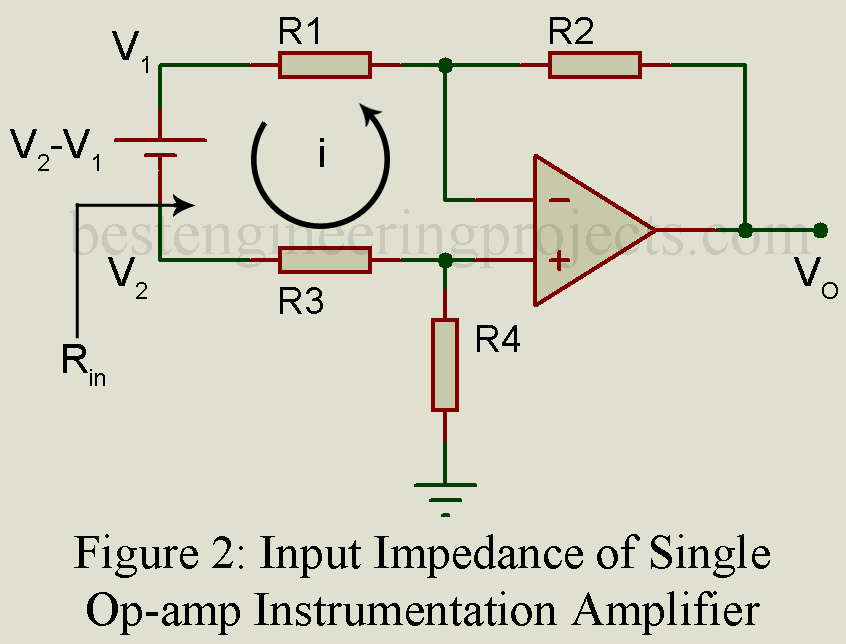
Input Impedance of single op-amp instrumental Amplifier

$\dfrac{R_4}{R_3} = \dfrac{R_2}{R_1}$ for common mode signal rejection.

$R_{in} = \dfrac{V_2-V_1}{i}$

$(V_2-V_1) = i\times R_3 + i\times R_1$

$\dfrac{V_2-V_1}{i} = R_1 + R_3$

$R_{in} = R_1 + R_3$

(For R₁ = R₃ and R₄ = R₂ then R_in = 2R₁)

Limitation of Single Op-Amp Instrumental Amplifier

Difficult to change gain because $\dfrac{R_2}{R_1} = \dfrac{R_4}{R_3}$ shall be maintain at the same time. and for large gain R₁ shall be kept relatively small which means input impedance decreases causing source overloading.

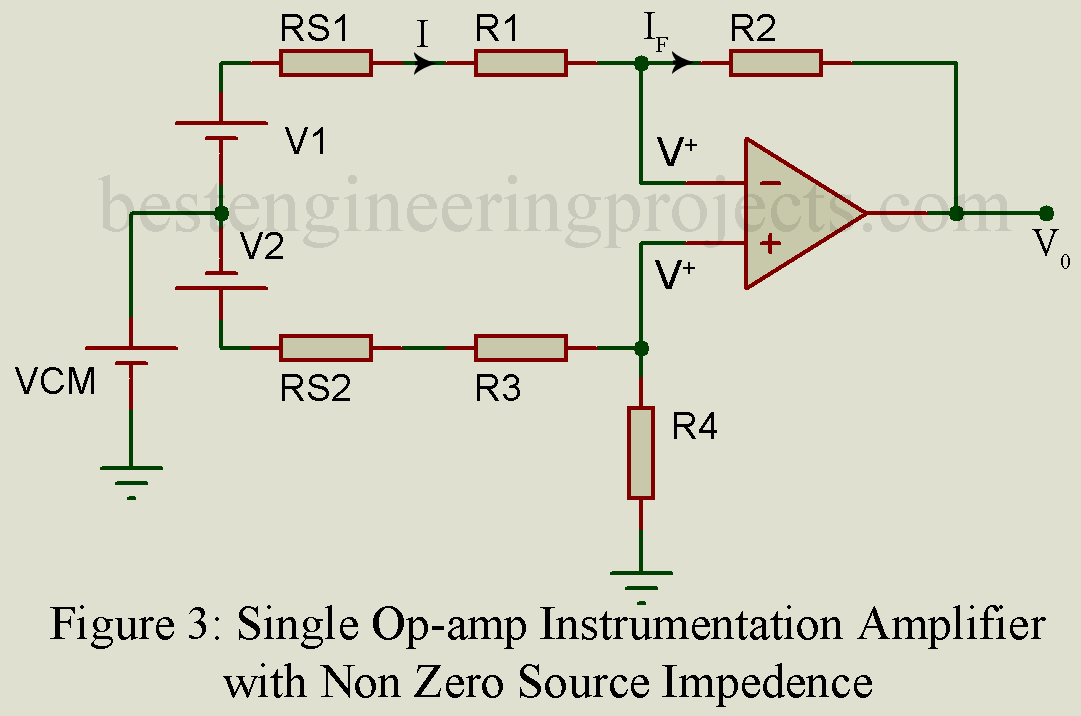
Single Op-amp Instrumental Amplifier with non-zero source impedance

$V^+ = \dfrac{R_4}{R_3+R_{s2}+R_4}\times (V_2+V_{cm})$ ……(4)

$I = I_f$

$\dfrac{V_{cm}+V_1-V^+}{R_1+R_{s1}} = \dfrac{V^+-V_0}{R_2}$ ……(5)

From equation 4 and 5, eliminating V⁺

$V_0 = (\dfrac{R_4}{R_{12}+R_3+R_4}-\dfrac{R_2}{R_{s1}+R_1}+\dfrac{R_2}{R_{s1}+R_1}-\dfrac{R_4}{R_{s1}+R_3+R_4})V_{CM}+\dfrac{R_4}{R_{s2}+R_3+R_4}\times(1+\dfrac{R_2}{R_{s1}+R_1})V_2-\dfrac{R_2}{R_{s1}R_1}V_1$ …..(6)

For complete rejection of common mode signal, V_cm containing term shall be zero.

$\dfrac{R_4}{R_{s2}+R_3+R_4}-\dfrac{R_2}{R_{s1}+R_1}+\dfrac{R_2}{R_{s1}+R_1}\times \dfrac{R_4}{R_{s2}+R_3+R_4} = 0$

$\dfrac{R_1+R_{s1}}{R_2} = \dfrac{R_3+R_{s2}}{R_4}$

$\dfrac{R_2}{R_1+R_{s1}} = \dfrac{R_4}{R_3+R_{s2}}$

From equation (3) $V_0 = \dfrac{R_2}{R_1+R_{s1}}\times (V_2-V_1)$

If source impedance are unequal common mode rejection is degraded.

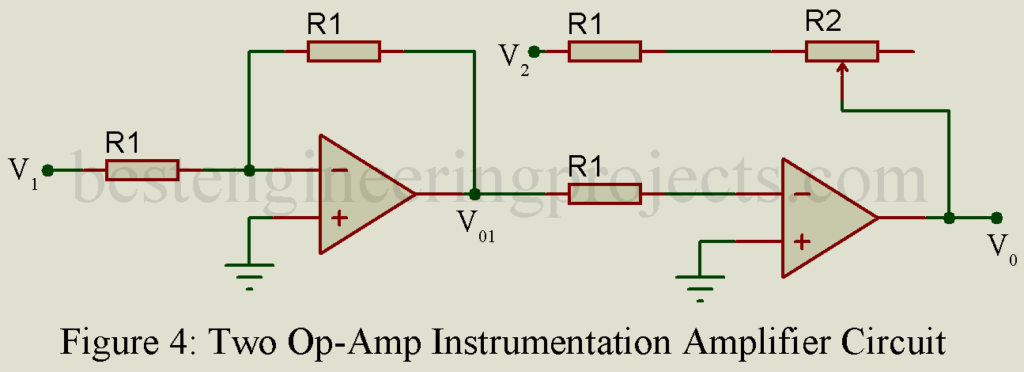
Two Op-Amp Instrumental Amplifier

Both the amplifier are configured in inverting mode.

$V_{01} = \dfrac{-R_1}{R_1}\times V_1 = -V_1$

$V_0 = \dfrac{-R_2}{R_1}\times V_2 \dfrac{-R_2}{R_1}\times V_{01}$

$V_0 = \dfrac{-R_2}{R_1}\times (V_2-V_1)$

Gain can be adjusted by adjusting variable resistor R₂
For good CMRR (Common mode rejection ratio) four resistors shall be matched.
For high input impedance input shall be given in non-inverting terminal.

$V_{01} = (1+\dfrac{R_2}{R_1})\times V_1$

$V_0 = (1 + \dfrac{R_4}{R_3})\times V_2-\dfrac{R_4}{R_3}\times V_{01}$

$V_0 = (1+\dfrac{R_4}{R_3})\times V_2-\dfrac{R_4}{R_3}\times (1+\dfrac{R_2}{R_1})\times V_1$

If $\dfrac{R_4}{R_3} = \dfrac{R_2}{R_1}$

$V_0 = (! + \dfrac{R_2}{R_1})\times (V_2-\dfrac{R_2}{R_1}\times V_1)$

It has a high input impedance.

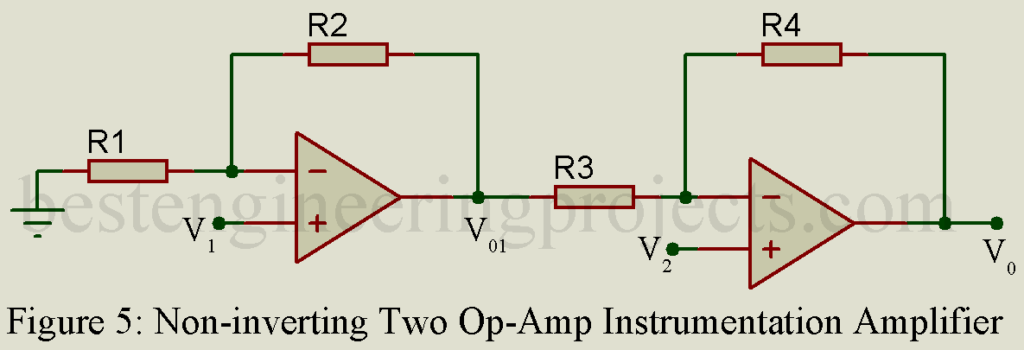
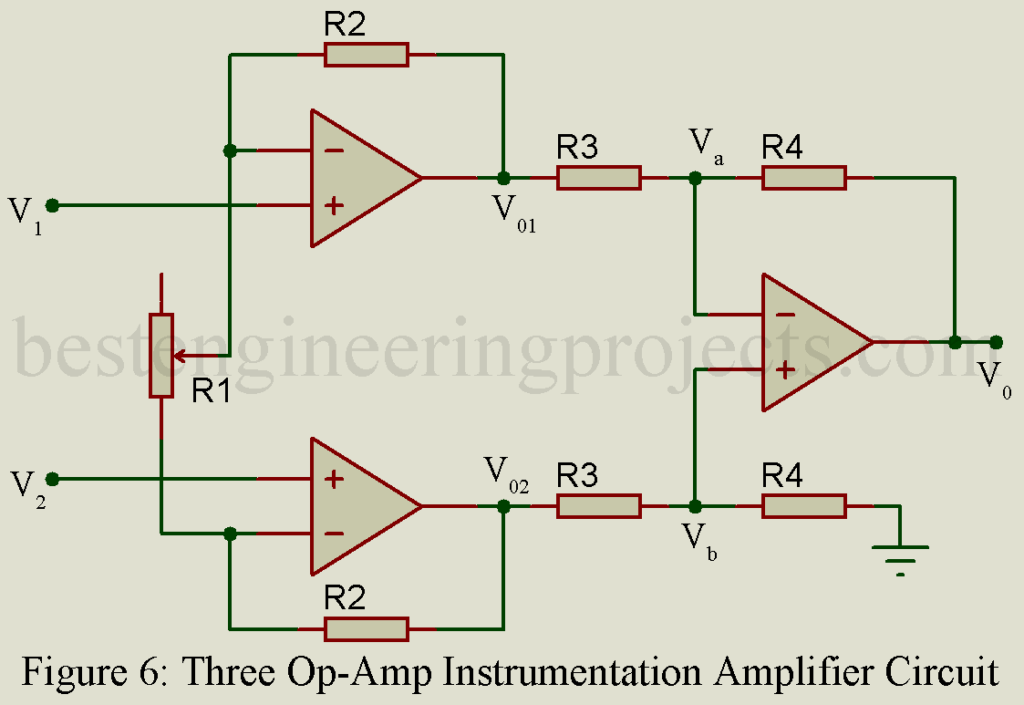
Three Op-amp Instrumental amplifier

In this circuit three OP-Amp are used and a potentiometer is provided to permit adjusting the scale factor of circuit, then from above diagram we can write

$\dfrac{V_{01}-V_1}{R_2} = \dfrac{V_1-V_2}{R_1}$ …..(7)

Or, $\dfrac{V_{01}}{R_2} = \dfrac{V_1}{R_1}+\dfrac{V_1}{R_2}-\dfrac{V_2}{R_1}$

Or, $V_{01} = \dfrac{R_2}{R_1}\times V_1 + V_1-\dfrac{R_2}{R_1}\times V_2$

Or, $V_{01} = V_1 + \dfrac{R_2}{R_1}\times [V_1-V_2]$ …..(8)

Similarly,

$\dfrac{V_2-V_{02}}{R_2} = \dfrac{V_1-V_2}{R_1}$

$-\dfrac{V_{02}}{R_2} = \dfrac{V_1}{R_1}-\dfrac{V_2}{R_2}-\dfrac{V_2}{R_1}$

$\dfrac{V_{02}}{R_2} = \dfrac{V_2}{R_2} + \dfrac{V_2}{R_1}-\dfrac{V_1}{R_1}$

$V_{02} = V_2 + \dfrac{R_2}{R_1}\times V_2-\dfrac{R_2}{R_1}\times V_1$

$V_{02} = V_2 + \dfrac{R_2}{R_1}\times [V_2-V_1]$ ……(9)

Now, for equation 2 and 4,

$V_{01}-V_{02} = V_1 + \dfrac{R_2}{R_1}\times [V_1-V_2]-V_2-\dfrac{R_2}{R_1}\times [V_2-V_1]$

$= V_1-V_2+\dfrac{R_2}{R_1}\times V_1-\dfrac{R_2}{R_1}\times V_2-\dfrac{R_2}{R_1}\times V_2 + \dfrac{R_2}{R_1}\times V_1$

$V_1-V_2+2\times \dfrac{R_2}{R_1}\times V_1-2\times \dfrac{R_2}{R_1}\times V_2$

$V_1-V_2 + 2\times \dfrac{R_2}{R_1}\times [V_1-V_2]$

$V_{01}-V_{02} = (V_1-V_2)\times [1 + 2\times \dfrac{R_2}{R_1}]$ ………(10)

Now applying KCL at node V_a, one can write

$\dfrac{V_a-V_{01}}{R_3}+\dfrac{V_a-V_o}{R_4} = 0$

$\dfrac{V_a}{R_3}+\dfrac{V_a}{R_4}-\dfrac{V_{01}}{R_3}-\dfrac{V_0}{R_4} = 0$

$\dfrac{V_0}{R_4} = \dfrac{V_a}{R_3}+\dfrac{V_a}{R_4}-\dfrac{V_{01}}{R_3}$

$\dfrac{V_a}{R_3}+\dfrac{V_a}{R_4} = \dfrac{V_0}{R_4}+ \dfrac{V_{01}}{R_3}$

$V_a\times (\dfrac{R_3+R_4}{R_3R_4}) = \dfrac{V_0}{R_4}+\dfrac{V_{01}}{R_3}$

$V_a = [\dfrac{R-3}{R_3+R_4}\times V_0 + \dfrac{R_4}{R_3+R_4}\times V_{01}]$ ……(11)

Similarly, applying kcl at node V_b,

$\dfrac{V_b-V_{02}}{R_3}+\dfrac{V_b}{R_4} =$

$\dfrac{V_b}{R_3} + \dfrac{V_b}{R_4}-\dfrac{V_{02}}{R_3} = 0$

$V_b\times (\dfrac{R_3+R_4}{R_3R_4}) = \dfrac{V_{02}}{R_3}$

$V_b = \dfrac{R_4}{R_3 + R_4}\times V_{02}$ ……(12)

For perfect balance, V_a must be equal to V_b. Thus, one can write as

V_a = V_b

$\dfrac{R_3}{R_3+R_4}\times V_0 + \dfrac{R_4}{R_3 + R_4}\times V_{01} = \dfrac{R_4}{R_3+R_4} \times V_{02}$

$\dfrac{R_3}{R_3+R_4}\times V_0 = \dfrac{R_4}{R_3+R_4}\times V_{02}-\dfrac{R_4}{R_3+R_4}\times V_{01}$

$\dfrac{R_3}{R_3+R_4}\times V_0 = \dfrac{R_4}{R_3+R_4} \times [V_{02}-V_{01}]$

$V_0 = \dfrac{R_4}{R_3}\times [V_{02}-V_{01}]$

$V_0 = -\dfrac{R_4}{R_3}\times [V_{01}-V_{02}]$ …….(13)

From equation 12 and 13 we can write

$V_0 = -\dfrac{R_4}{R_3}\times [V_1-V_2]\times [1+ 2\times \dfrac{R_2}{R_1}]$

$V_0 = \dfrac{R_4}{R_3}\times [V_2-V_1]\times [1 + 2\times \dfrac{R_2}{R_1}]$ ……(14)

This gain can be expressed as

$A_v = \dfrac{V_0}{(V_2-V_1)}$

$A_v = \dfrac{R_4}{R_3}[1+ 2\times \dfrac{R_2}{R_1}]$ …..(15)

The equation 14 yields an output and that equation 15, provides gain of an instrumentation amplifier.

3 Op-amp Instrumentation amplifier has two stages in which 1^st stage provides high input impedance (ideally infinity) because both input are at non-inverting terminals. Second stage completely rejects common mode signal i.e. high CMRR, because $\dfrac{R_4}{R_3} = \dfrac{R_4}{R_3}$ . Gain can be verified by changing variable resistor R₂.