Forced Vibration of a Mass Spring System with Damping

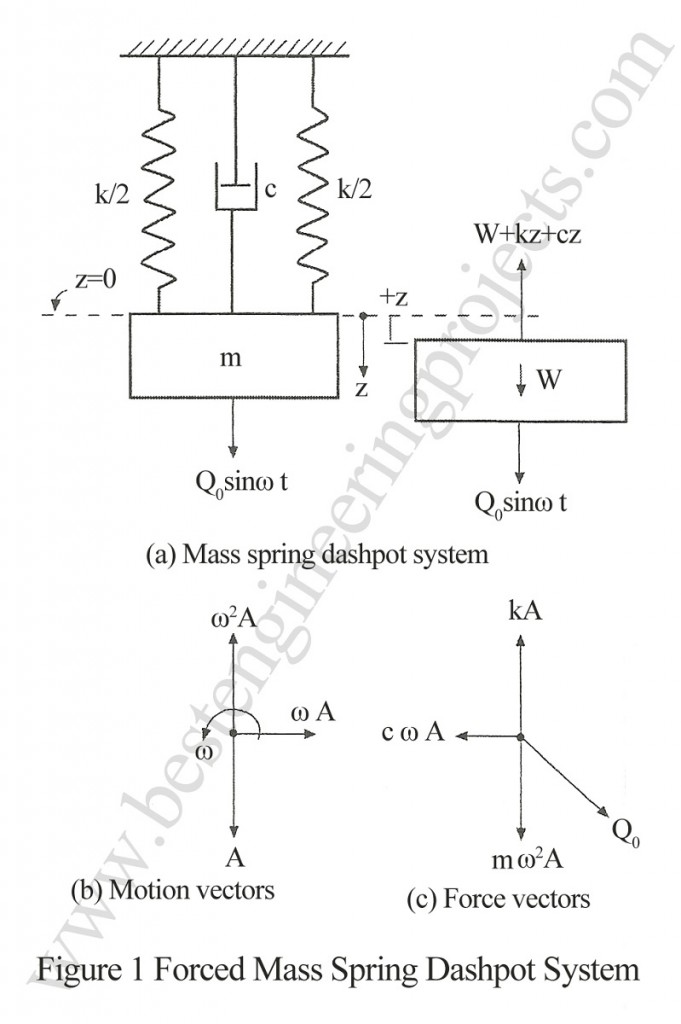
In foundation soil system damping is always present in one form or another. For this case fig. 1 (a), the equation of motion is:

$W-(W+kz)-c\dfrac{dz}{dt}+Q_0Sin\omega t=m\dfrac{d^2z}{dt^2}$ ———-(1)

$m\dfrac{d^2z}{dt^2}+c\dfrac{dz}{dt}+kz=Q_0Sin\omega t$ ———-(2)

The solution of equation (2) is done by applying the concept of rotating vector. In the figure 1 the exciting force vector Q₀ is placed with a phase angle $\phi$ ahead of the displacement vector A. The equation of displacement may be expressed as:

$z=Sin(\omega t -\phi)$ ———-(3)

In figure 1 (b) the position of motion vector is shown. In figure 1 (c) the position of force vector is shown. The force vectors act opposite to that of motion vectors. The force vector Q₀ is placed with a phase angle $\phi$ ahead of the displacement vector A resolving the force in the vertical and horizontal direction, we have,

$kA=m\omega^2A-Q_0cos\phi=0$ ———-(4)

And $c\omega A-Q_0sin\phi=0$ ———-(5)

Solving for A and $\phi$ we have,

$A=\dfrac{Q_0}{\sqrt{(k-m\omega^2)^2 +(c\omega)^2}}$ ———-(6)

And $tan\phi = \dfrac{c\omega}{k-m\omega^2}$ ———-(7)

$A=\dfrac{\dfrac{Q_0}{k}}{\sqrt{\left(1-\dfrac{m}{k}\omega^2\right)^2+\left(\dfrac{c\omega}{k}\right)^2}}$

$A=\dfrac{\dfrac{Q_0}{k}}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 + \left(Dc_c\dfrac{\omega}{k}\right)^2}}$

$A=\dfrac{\dfrac{Q_0}{k}}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 + 4D^2m^2\dfrac{\omega^2}{k^2}}}$

$A=\dfrac{\dfrac{Q_0}{k}}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 + \left(2D\dfrac{\omega}{\omega_n}\right)^2}}$ ———-(8)

$M=\dfrac{A}{\dfrac{Q_0}{k}}=\dfrac{1}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 + \left(2D\dfrac{\omega}{\omega_n}\right)^2}}$ ———-(9)

$tan\phi=\dfrac{2D\dfrac{\omega}{\omega_n}}{1-\left(\dfrac{\omega}{\omega_n}\right)^2}$ ———-(10)

$Q_0=A\times\sqrt{\left((k-m\omega)^2+(c\omega)^2\right)}$ ———-(11)

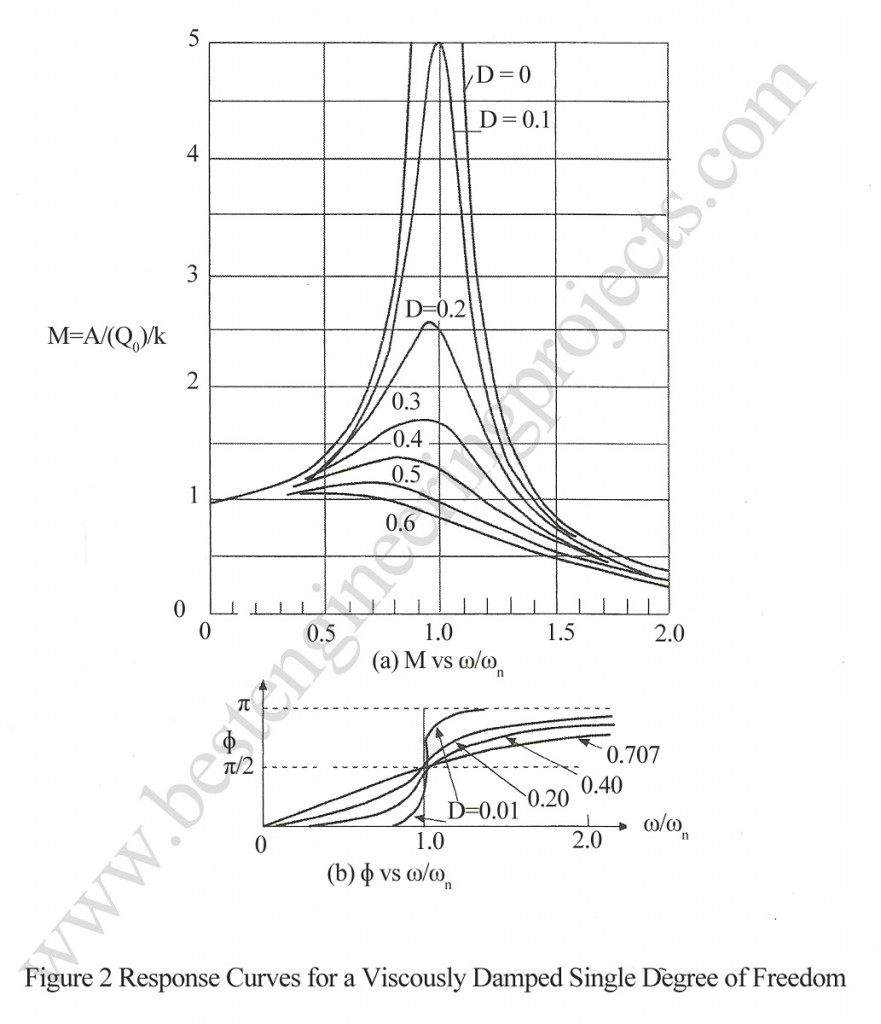
The equations are plotted for various values D as shown in figure 2(a) and (b). These curves are referred to here as response curves for Constant-force-amplitude-excitation. In the figure it is seen that maximum amplitude occurs at a frequency slightly less than the undamped natural circular frequency, $\omega_n$ where $\dfrac{\omega}{\omega_n}=1$ . The frequency at maximum amplitude will be referred to as resonant frequency f_m for constant force Q₀.

Resonant frequency at maximum amplitude

$M=\dfrac{A}{\dfrac{Q_0}{k}}=\dfrac{1}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 + \left(2D\dfrac{\omega}{\omega_n}\right)^2}}$ ———-(12)

Put $x=\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 + \left(2D\dfrac{\omega}{\omega_n}\right)^2$ and $a=\dfrac{\omega}{\omega_n}$ , then