Forced Frequency Dependent Exciting Force with Viscous Damping

Engineeering Projects

Introduction to Forced Frequency Dependent Exciting Force with Viscous Damping

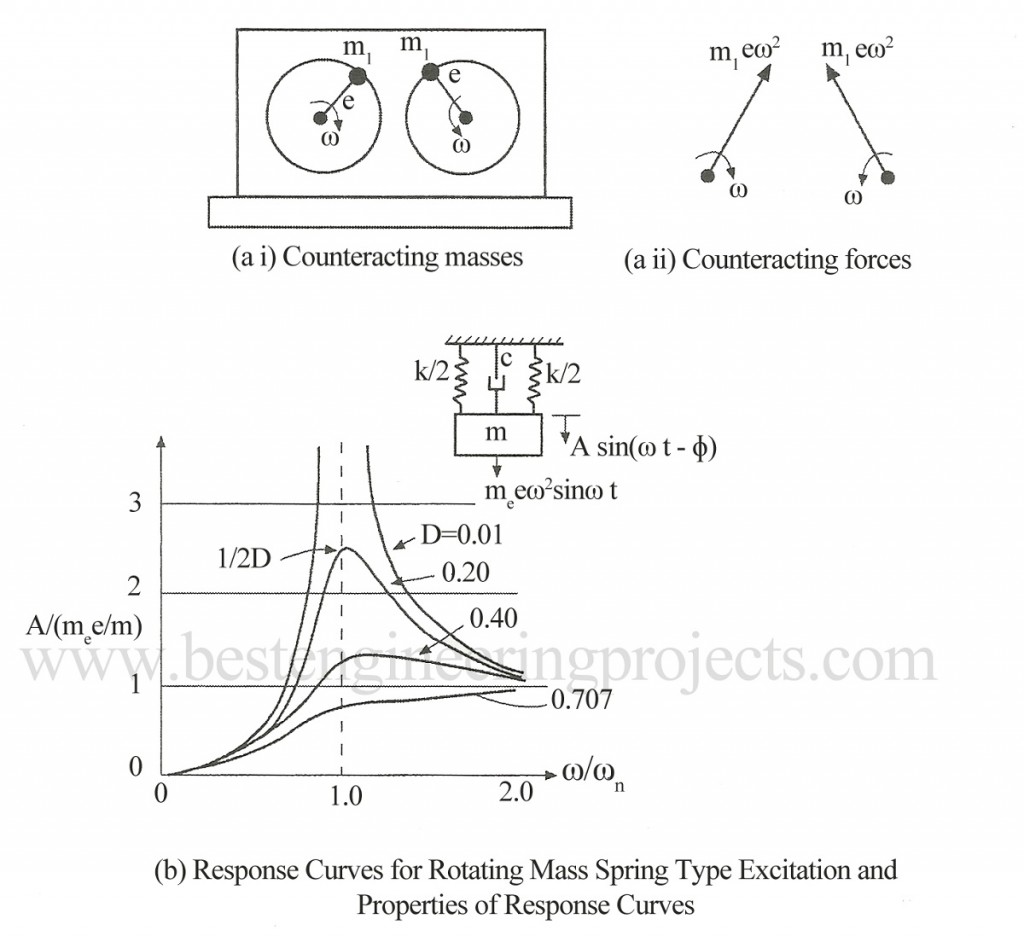
Some machines like Turbo-generators produce unbalanced force which imparts into the foundation-soil system frequency dependent exciting force. In Turbo generators two counteracting masses are placed at an eccentricity, e. This is shown in Figs. 1(a) and (b).

response curve for rotating spring type excitation and properties of response curve

The masses are so placed that they reach the top simultaneously. The rotating force of each mass is given by,

Q_1=m_1\times e\times\omega^2  ———-(1)

Referring to the figure and resolving the force horizontally and vertically we got the total vertical force as:

Q_v = 2Q_1 = 2m_1 \times e \omega^2 = m_e \times e \omega^2    ———-(2)

And horizontal forces cancel each other. The vibrating force at any position is given by

Q = m_e\times e\times\omega^2 Sin\omega t = Q_0 Sin\omega t  ———-(3)

Where, Q_0 = m_e \times e\times\omega^2  ———-(4)

Thus the periodic force can be expressed as,

Q = Q_0sin\omega t  ———-(5)

We, have,

\dfrac{Q_0}{k}=\dfrac{m_e\times e\times\omega^2}{k}=\dfrac{m_e\times e}{m}\times\dfrac{m}{k}\times\omega^2=\dfrac{m_e\times e}{m}\left(\dfrac{\omega}{omega_n}\right)^2

We know,

A=\dfrac{\dfrac{Q_0}{k}}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 +\left(2D\dfrac{\omega}{\omega_n}\right)^2}}  ———-(6)

Or, A=\dfrac{\dfrac{m_e\times e}{m}\left(\dfrac{\omega}{\omega_n}\right)^2}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 +\left(2D\dfrac{\omega}{\omega_n}\right)^2}}  ———-(7)

Or, \dfrac{A}{\dfrac{m_e\times e}{m}}= \dfrac{\left(\dfrac{\omega}{\omega_n}\right)^2}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2 +\left(2D\dfrac{\omega}{\omega_n}\right)^2}}=M\times \left(\dfrac{\omega}{\omega_n}\right)^2   ———-(8)

Where, M is the dynamic magnification factor for constant force amplitude case. Fig.1 (b) shows a plot of above equation for various of D. The curves are obtained by multiplying amplitude for each value of \dfrac{\omega}{\omega_n} by a factor of \left(\dfrac{\omega}{\omega_n}\right)^2. In this case the damped resonant frequency fmr occurs above the undamped natural frequency fn. The relation between the two is derived as follows.

\dfrac{A}{\dfrac{m_c\times c}{m}}= \dfrac{\left(\dfrac{\omega}{\omega_n}\right)^2}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2+\left(2D\dfrac{\omega}{\omega_n}\right)^2}}  ———-(9)

Put x=\sqrt{\dfrac{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2+\left(2D\dfrac{\omega}{\omega_n}\right)^2}{\left(\dfrac{\omega}{\omega_n}\right)^4}} and a=\dfrac{\omega}{\omega_n}, then

x=\sqrt{\dfrac{(1-(a)^2)^2+(2Da)^2}{a^4}}

 

x=\sqrt{\left(\dfrac{1}{a^2}-1\right)^2+\left(\dfrac{2D}{a}\right)^2}  ———-(10)

\dfrac{dx}{da}=2\left(\dfrac{1}{a^2}-1\right)(-2)a^{-3}+\left(\dfrac{2\times 2D}{a}\times 2D\right)\times (-1)a^{-2}=0 \dfrac{dx}{da}=0

Or, \dfrac{1}{a^2}-1+2D^2=0

Or, \dfrac{1}{a^2}=1-2D^2

Or, a^2=\dfrac{1}{1-2D^2}

Or, a=\dfrac{1}{\sqrt{1-2D^2}}  ———-(11)

Or, \dfrac{\omega}{\omega_n}=\dfrac{1}{\sqrt{1-2D^2}}[/latex]  ———-(12)

Taking positive sign, we get,

\omega=\omega_n\dfrac{1}{\sqrt{1-2D^2}}  ———-(13)

f_{mr}=f_n\dfrac{1}{1-2D^2}

f_{mr}=\dfrac{1}{2\pi}\sqrt{\dfrac{k}{m}}\dfrac{1}{1-2D^2}  ———-(14)

Relation between M and D at resonant frequency

We know,

\dfrac{A}{\dfrac{m_c\times c}{m}}= \dfrac{\left(\dfrac{\omega}{\omega_n}\right)^2}{\sqrt{\left(1-\left(\dfrac{\omega}{\omega_n}\right)^2\right)^2+\left(2D\dfrac{\omega}{\omega_n}\right)^2}} = M\times\left(\dfrac{\omega}{\omega_n}\right)^2   ———-(15)

When, \dfrac{\omega}{\omega_n}=1,

M = \dfrac{A}{\dfrac{m_c\times c}{m}}=\dfrac{1}{2D}   ———-(16)

When damping in the system is neglected, then

M=\dfrac{a^2}{1-a^2}

In practice, the amplitude at resonance will be finite because of damping which is inherently in any physical system. It is however desirable to ensure in the design of any dynamically loaded structure that the value of frequency ratio ‘a’ is far from unity. As per IS Code the working range of frequency ration is given by the inequality

1.4\leq a \leq 0.5

Maximum magnification factor of vibration

In this case the maximum magnification factor will be M_{max}=\dfrac{1}{2D\sqrt{1-D2}} and is same in constant force amplitude case. When D is too small, then M_{max}=\dfrac{1}{2D}, this is same as above. Thus if we have a value of damping ratio D, we can get a quick estimate of the probable magnification factor by which the static deflection must be multiplied to given the maximum dynamic motion of the footing. For D = 0.20 the magnification factor will be 2.5, for D = 0.10 the magnification factor will be 5, for D = 0.05 the magnification factor will be 10. For D is greater than 0.20 the equation for Mmax should be used.

Leave a Comment