Effect of Sloping Surcharge in Passive Case

August 28, 2013May 3, 2021 Engineeering Projects

What are Effect of Sloping Surcharge in Passive Case?

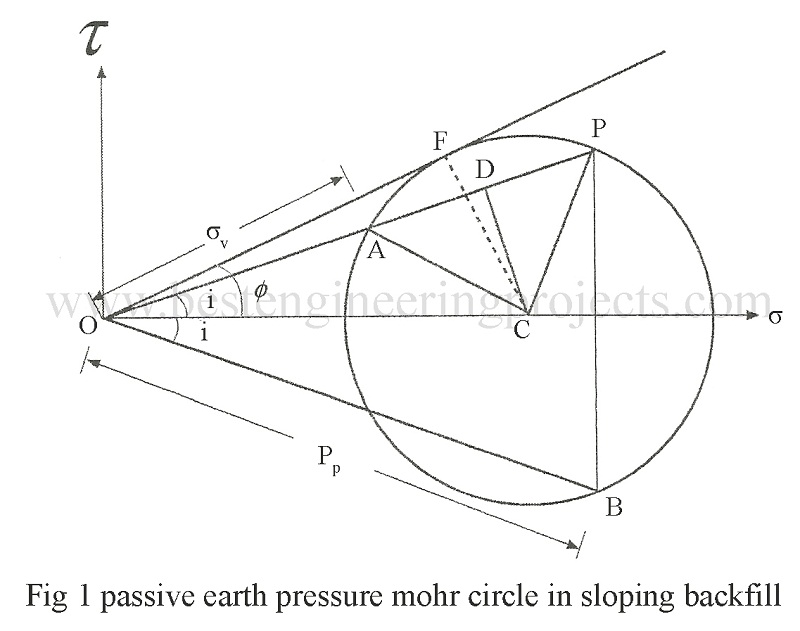
In previous article we had already posted Effect of Sloping Surcharge in Active Case, now in this article we are dealing with Effect of Sloping Surcharge in Passive Case. The Mohr Circle for the passive case of a retaining wall carrying a sloping backfill is shown in Fig.1. Consider an element subjected to a stress in the $\sigma_v$ in the vertical direction and $\sigma_x$ in the direction parallel to the backfill. As these stresses in one plane are parallel to the direction of another plane, these stresses are conjugate stresses and the planes are the conjugate planes.

The equivalent vertical stress-acting acting parallel to the surface of backfill is given by

$\sigma_{ve} = \sigma_vcosi = \gamma z cosi$

Referring to the figure the coefficient of passive earth pressure can be written as:

$K_p=\dfrac{\sigma_x}{\sigma_{ve}}=\dfrac{\sigma_p}{\sigma_vcosi}$

$= \dfrac{OP}{OA}$

$= \dfrac{OD + PD}{OD - AD}$

$=\dfrac{OD+PD}{OD-PD}$

We can also write:

CD = OC sini

OD = OC cosi

$PD=\sqrt{PC^2-CD^2}$

$PD=\sqrt{R^2-CD^2}$

$R = OC sin\phi$

By substitution these values in the expression for K_p we get:

$K_p=\dfrac{OCcosi+\sqrt{OC^2sin^2\phi-OC^2sin^2i}}{OCcosi-\sqrt{OC^2sin^2\phi-OC^2sin^2i}}$

$K_p=\dfrac{cosi+\sqrt{sin^2\phi-sin^2i}}{cosi-\sqrt{sin^2\phi-sin^2i}}=\dfrac{cosi+\sqrt{cos^2i-cos^2\phi}}{cosi-\sqrt{cos^2i-cos^2\phi}}$

$P_P = K_p\gamma z cosi$

$K_P = K_P cosi$ ———–(1)

Where,

$K_p=cosi\left[\dfrac{cosi+\sqrt{cos^2i-cos^2\phi}}{cosi-\sqrt{cos^2i-cos^2\phi}}\right]$

And is known as the coefficient of passive earth pressure.

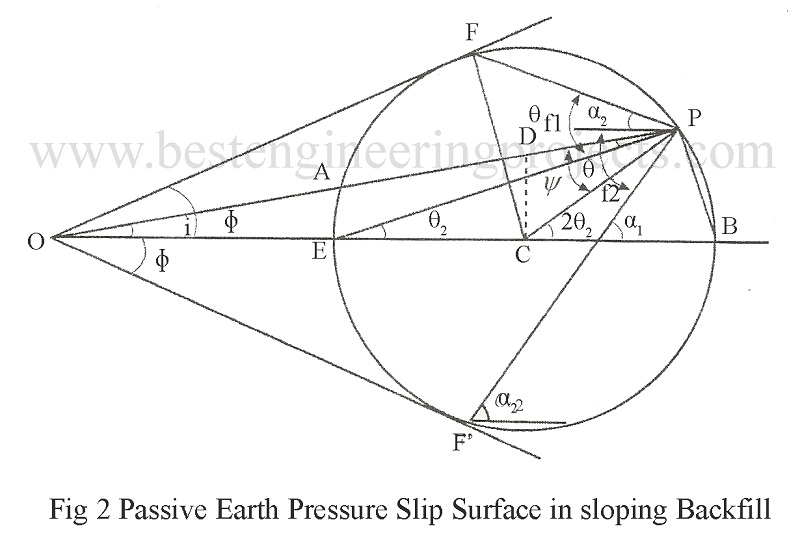
If, $\alpha_1$ and $\alpha_2$ are the inclination of failure planes with horizontal as shown in figure 2 then,

$\theta_{f2} = \alpha_1-\theta_2$

$\alpha_1 = \theta_{f2} + \theta_2$

$\psi = -i+2\theta_2$ $\theta_2=\dfrac{(\psi-i)}{2}$

But, $\theta_{f2}=45^0-\dfrac{\phi}{2}$

Hence, $\alpha_1=45^0-\dfrac{\phi}{2}+\dfrac{\psi+i}{2}$

And Similarly, $\alpha_2=45^0-\dfrac{\phi}{2}-\dfrac{\psi+i}{2}$

Where, $sin\psi=\dfrac{CD}{CP}=\dfrac{CD}{CF}=\dfrac{OCsini}{OCsin\phi}$ CD normal to OA

and $\psi=sin^{-1}\dfrac{sini}{sin\phi}$

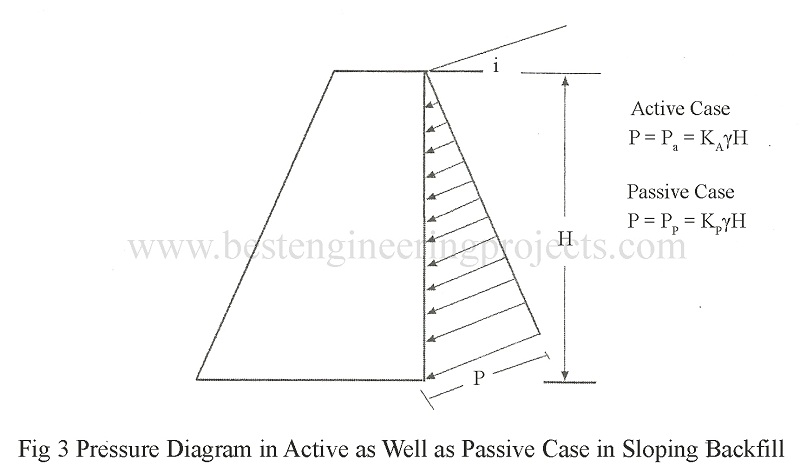
The pressure diagram is shown in figure 3 for both active as well as passive cases.

Leave a Comment Cancel reply