Development of equation of Bearing Capacity by Prandtl

Engineeering Projects

How to Development of equation of Bearing Capacity by Prandtl?

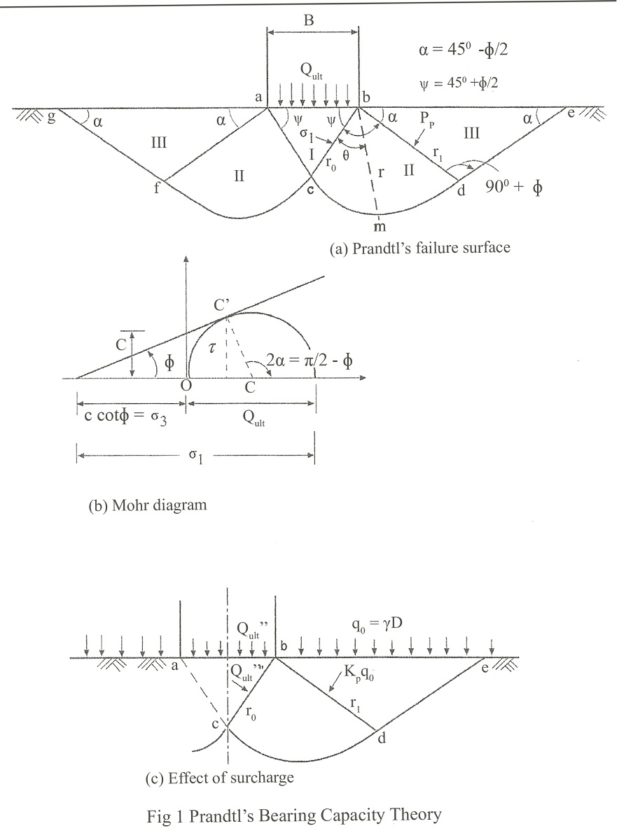
equation of Bearing Capacity by Prandtl: As failure surfaces are symmetrical only forces acting on the right side of the wedges are considered. According to Prandtl, the bearing pressure Qult acting at the base ab of the footing is transmitted through the soil wedge abc on to the face bc, according to the Pascal’s law, pressure is undiminished and same in all direction. The state of stress within the wedge on the line bc may be explained with respect to Mohr diagram (Fig.1 b).

  • The initial stress in the soil is equal to

c cot\phi = P_i

This stress acts normal to the face bc and is considered as the minor principal stress \sigma_3.

  • The bearing pressure Qult is also assumed to act normal to the face bc of the wedge according to the Pascal’s law,
  • The total pressure acting on the face bc is equal to Qult + Pi which is considered as the major principal stress \sigma_1.

Thus we may write, \sigma_1 = Q_{ult} + P_i

\sigma_3 = P_i

According to the relation between principal stresses at failure we can write,

\dfrac{\sigma_1}{\sigma_3} = K_p = \dfrac{1 + sin\phi}{1-sin\phi}

Or, \sigma_1 = \sigma_3 tan^2 (45^0 + \dfrac{\phi}{2})  ———- (1)

Where, Kp is the passive earth pressure coefficient. Substituting the values of major and minor principal stresses \sigma_1 and \sigma_3 we get,

Q_{ult} + P_i = p_iK_p   ———- (2)

When the wedge abc is pushed down, it pushes the soil within the radial shear Zone bcd. If bc is assumed as retaining wall, the soil within the elastic wedge expands and tends to away from bc due to active pressure acting along bc. The active pressure is given by,

P_a = Q_{ult} + p_i   ———- (3)

Which is same the equation derived as before. The total active force on be is given by:

P_a = bc\times p_a = bc \times (Q_{ult} + p_i)  ———- (4)

The equation to the spiral cd with the pole at b may be written as:

r = r_0 \times e^{\theta tan \phi}   ———- (5)

Where, r0 = the initial radius vector bc

r = the radius vector bm of any point m on the spiral cd where r makes an angle \theta with r0.

Substituting r0 in Eq.(4) We get,

P_a = r_0 \times (Q_{ult} + p_i)   ———- (6)

prandtl's bearing capacity theory

The action of pushing to the soil in the radial shear zone by bc also tends to push the soil in Zone III as Well. This effect is resisted by the soil in Zone III and a passive resistance is developed along bd, which also acts as a retaining wall. If Pp is the passive resistance per unit area of bd, then we can write,

P_p = bd \times p_p = r_1 \times p_p   ———-(7)

Since the stresses get distributed hydrostatically, unit active pressure must equal to the unit passive pressure. Then,

P_p = p_a = Q_{ult} + p_i

= K_p \times P_i   ———- (7)

Taking moment of the active and passive forces at b we get,

p_ar_0 \times \dfrac{r_0}{2} = p+pr_1 \times \dfrac{r_1}{2}

Or, p_ar_0^2 = p_pr_1^2

Or, (Q_{ult} + p_i) \times r_0^2 = p_iK_p \times (r_0 \times e^{\theta tan \phi})^2

Or, Q_{ult} + p_i = p_ik_p \times e^{2\theta tan \phi}

Or, Q_{ult} + p_i = p_ik_p \times e^{\dfrac{2\pi}{2}tan \phi}

Or, Q_{ult} = p_i(k_p \times e^{\pi tan \phi}-1)

Or, Q_{ult} = c cot \phi (k_p e^{\pi tan \phi}-1) = cN_c  ———- (8)

Where, N_c = cot \phi (k_p e^{\pi tan \phi}-1)

This is the original equation derived by Prandtl. This equation does not take the surcharge into account. Taylor 1948 extended the theory of Prandtl to account for surcharge.

Prandtl equation with surcharge effect – Figure 1 c shows a footing subjected to a surcharge q0. The ultimate bearing capacity including surcharge can be written as:

Qult = Q’ult + Q”ult   ———- (9)

Where,

Q’ult = Ultimate bearing capacity without surcharge

Q”ult = Additional bearing capacity due to surcharge

The equation for Q”ult can be obtained in the similar manner as was obtained for Qult. In this case the unit normal stress acting on face bc is Q”ult and that acting on face bd is Kpq0. Taking moment as before we get,

Q"_{ult} r_0 \times \dfrac{r_0}{2} = K_pq_0r_1 \times \dfrac{r_1}{2}   ———-(10)

Q"_{ult} = K_pq_0 \times (\dfrac{r_1}{r_0})^2

Q"_{ult} = K_pq_0e^{\pi tan \phi}   ———- (11)

The total ultimate bearing capacity may now be written as:

Q_{ult} = c cot\phi [K_p e^{\pi tan \phi}-1] + K_pq_0e^{\pi tan \phi} ———- (12)

Or, Q_{ult} = cN_c + q_0N_q   ——— (13)

Where, N_c = c cot\phi (N_q-1)   ———- (14)

N_q = K_p e^{\pi tan \phi} ———- (15)

Where, Nc and Nq are called the bearing capacity factors.

Comments on Prandtl’s Equation – Where c = 0 the ultimate bearing capacity is zero. The equation does not take account the width of the foundation. It also does not consider the weight of the failure wedge. When \phi = 0, the ultimate bearing capacity is infinity which is quite far from reality.

Leave a Comment