Load Carrying Capacity Pile

Engineeering Projects

There are various methods of determining the load carrying capacity of single piles. They are:

  • By Static Bearing Capacity Equations
  • Based on SPT Results
  • Based on CPT Results
  • By Pile Driving Formula
  • By Pile Loading Tests

Static Bearing Capacity Equations

The static methods give the ultimate bearing capacity of an individual pile, depending upon the characteristics of soil.

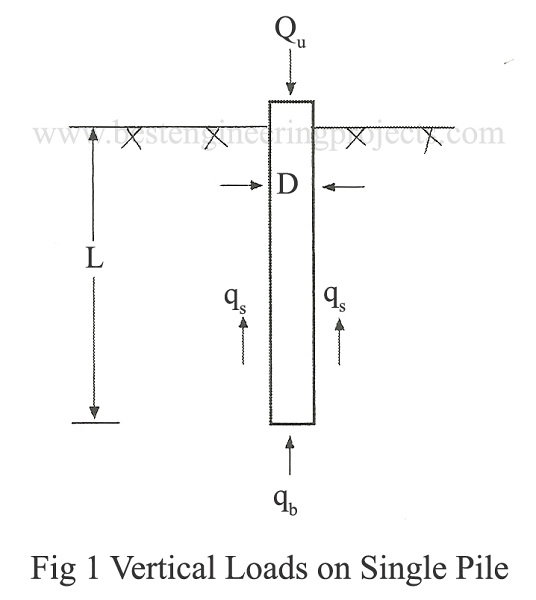
Assume a pile of diameter D is driven to a length L from the ground surface as shown in Fig.1. Let Qu be the net load applied at the head of the pile. The weight of pile is W and unit weight of soil is Y. If qb and qs are the unit base and skin friction respectively, then we can write the ultimate capacity of pile as:

Q_u + W-\gamma D_f = q_bA_b + q_sA_s   ———- (1)

vertical loads on single pile

If the weight of the pile and weight of the displaced soil are assumed as nearly equal we have:

Q_u = q_bA_b + q_sA_s

Then,  q_b = \dfrac{1}{2}B\gamma N\gamma + \sigma_v N_q + s_uN_c-\sigma_v

Or,     q_b = \dfrac{1}{2}B\gamma N\gamma + \sigma_v (N_q-1)+s_uN_c   ———- (2)

Similarly unit skin friction can be obtained as :

q_s = s_a + k\sigma_v tan\delta   ———- (3)

Where, \sigma_v is the effective normal stress acting alone the shaft of the pile and the variation of the normal stress is linear. sa is the adhesion between, pile and surrounding soil. The average effective normal stress is \dfrac{0+\sigma_v}{2} = \dfrac{\sigma_v}{2} = \sigma_v'

Hence,

q_s = s_a + K\sigma_v' tan\delta   ———- (4)

Therefore, the net ultimate pile capacity becomes:

Q_u = [\dfrac{1}{2}B\gamma N\gamma + \sigma_v(N_q-1)+s_uN_c]A_b + [s_a + K\sigma_v' tan\delta]A_s   ———- (5)

This is the general equation applicable to soil having both cohesion and friction.

Cohesionless soil – If soil is cohesionless, cohesion is zero and the Eq.(5) reduces to:

Q_u = \sigma_v(N_q-1)A_b + K\sigma_v' tan\delta A_s   ———- (6)

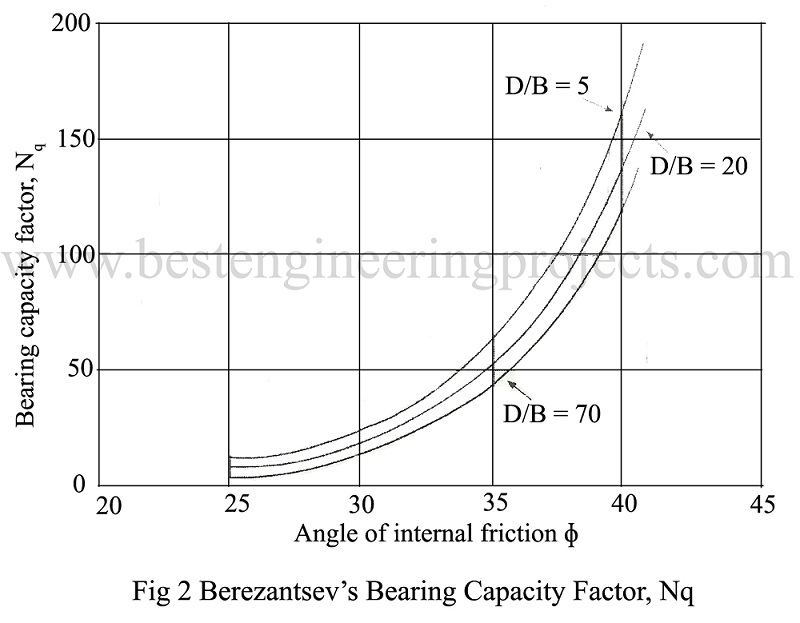
The Eq.(6) neglects the term \dfrac{1}{2}B\gamma N\gamma, since pile width is very small as compared to its length. The value of Nq is obtained by the relationship suggested by Berezantsev (1961), which is shown in Fig. To use the graph shown in Fig.2 the value of \phi should be known and this can be obtained from the results of Standard Penetration Test using the graph given in Fig.2. The suggested relation can only be used when piles are driven to depths greater than five times the pile width if less use Terzaghi’s bearing capacity equation. The term Nq is very sensitive to \phi a relative small error in estimating \phi will lead to much larger error in Nq.

Meyerhof has suggested that the bearing capacity of piles driven into loose sands can be doubled owing to compaction. The suggested value of K with \delta is given in Table 1 below.

Table 1 Values of K and \delta

Pile material

\delta

K

Loose

Dense

Steel

20

0.5

1

Concrete

0.75 \phi

1

2

Wood

0.67 \phi

1.5

3

 

Cohesive soil– In cohesive soil, the angle of internal friction is zero. Hence, the above Eq.(5) can be written as:

Q_u = s_uN_cA_b + s_aA_s   ———- (7)

In the above equation sa is the adhesion between pile and surrounding soil. Su is the undrained shear strength at base. Driving piles in clay reduces shear strength in many ways. If the reduction factor is \alpha then we can write:

\alpha = \dfrac{s_a}{s_u'}   ———- (8)

berezantsev's bearing capacity factor

Where, s_u' = Average undrained strength over the embedded length of pile

s_a = \alpha s_u'  ———- (9)

Hence from Eqs.(7) and (9)

Q_u = s_uN_cA_b + \alpha s_u'A_s ———- (10)

In the above equation, the value of Nc is taken equal to 9. In clayey soil base resistance is negligible. So an error in the estimation of base load is less significance. The main objective therefore is the determination of adhesion factor mobilized between pile and the surrounding clay.

Leave a Comment