h-parameter Model for Transistor

Transistor static characteristics curves are nonlinear. But for small signal operation, the point of operation moves about the quiescent operating point over a small range. Then the transistor parameters may be considered to be constant over this small range of operation.

Derivation of h-Parameter model for transistor

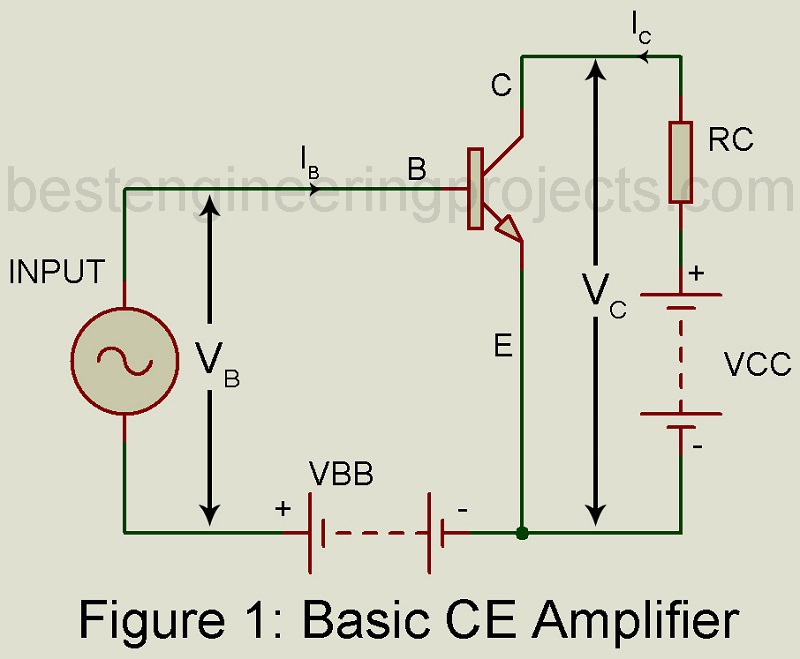
To drive the h-parameter model for a transistor, we consider the basic CE amplifier circuit of figure 1. The variable i_B, i_C, v_B (=v_BE) and v_C(v_CE) represent the instantaneous total values of currents and voltages. The input current i_B and output voltage v_C are chosen as the independent variables. Then varibles v_B and i_C are functions of i_B and v_C. we may write

$v_B = f_1 (i_B, v_C)$ …..(1)

$i_C = f_2 (i_B, v_C)$ …..(2)

Making Taylor series expansion of equation (1) and (2) about the zero signal operating point (I_B, V_c) and neglecting the higher order terms we get,

$\Delta v_B = \dfrac{\partial f_1}{\partial i_B}|_{v_C} \times \Delta i_B + \dfrac{\partial f_1}{\partial v_C}|_{I_B} \times \Delta v_C$ …..(3)

$\Delta i_C = \dfrac{\partial f_2}{\partial i_B}|_{V_C} \times \Delta i_B + \dfrac{\partial f_2}{\partial v_C}|_{I_B} \times \Delta v_C$ ……(4)

When partial derivatives $\dfrac{\partial f_1}{\partial i_B}$ and $\dfrac{\partial f_2}{\partial i_B}$ are taken keeping the collector voltage constant while partial derivatives $\dfrac{\partial f_1}{\partial v_C}$ and $\dfrac{\partial f_2}{\partial v_C}$ are taken keeping the base current constant.

Quantities $\Delta v_B$ , $\Delta i_C$ , $\Delta i_B$ and $\Delta v_C$ represent small increments in base and collector voltages and currents and may be represented by the symbols v_b, i_c, i_b and v_c respectively. Then we may rewrite Equations (3) and (4) as below:

$v_b = h_{ie} \times i_b + h_{re}\times v_c$ ……(5)

$i_c = h_{fe} \times i_b + h_{oe} \times v_c$ ……(6)

Where $h_{ie}\dfrac{\partial f_1}{\partial i_B} |_{V_c} = \dfrac{\partial v_B}{\partial i_B} |_{V_c} = \dfrac{i_c}{i_b}|_{V_c =0}$ …..(7a)

$h_{fe} = \dfrac{\partial f_2}{\partial i_B} |_{V_c} = \dfrac{\partial i_C}{\partial i_B}|_{V_c} = \dfrac{i_c}{i_b}|{V_c = 0}$ ……(7b)

$h_{re} = \dfrac{\partial f_1}{\partial v_C} |_{I_B} = \dfrac{\partial v_B}{\partial v_C} |_{I_B} = \dfrac{v_b}{v_c} |_{i_b = 0}$ ……(7c)

$= \dfrac{\partial f_c}{\partial v_C} |{I_B} = \dfrac{\partial i_C}{\partial v_C} |_{I_B} = \dfrac{i_c}{v_c} |{i_b=0}$ …..(7d)

The partial derivatives in Equations (7) define the h-parameters of the transistors in the CE configuration.

Parameters h_fe is the most important small signal parameters of a transistor and is called small signal $\beta$ , indicated by $\beta$ ‘ (as already defined earlier).

In case of sinusoidal voltage are currents, Equation (7a) becomes,

$h_{ie} = \dfrac{V_b}{I_b} |_{V_c =0}$ …..{8}

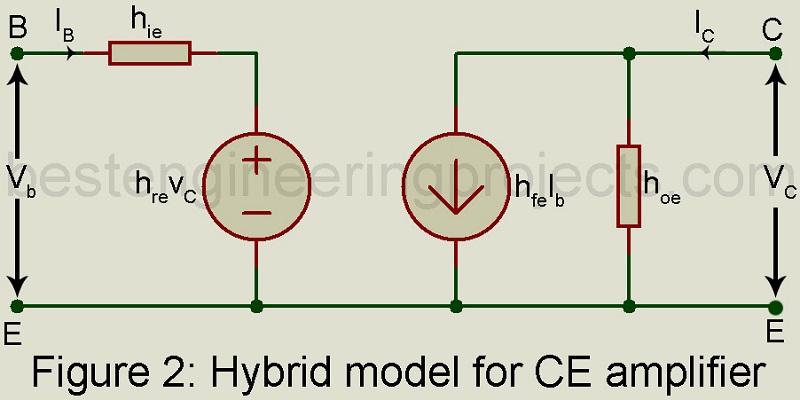
Figure 2 gives the h-parameter model for a transistor in CE configuration. Assuming sinusoidal voltages and currents, rms value I_b, I_c, V_b and V_c have been used. Exactly similar models may be drawn for CB and CE configurations using h-parameters relevant for the configurations.

The model of Equation (3) and the corresponding equations are valid for both PNP and NPN transistors and are independent of the load impedance of the method of biasing.

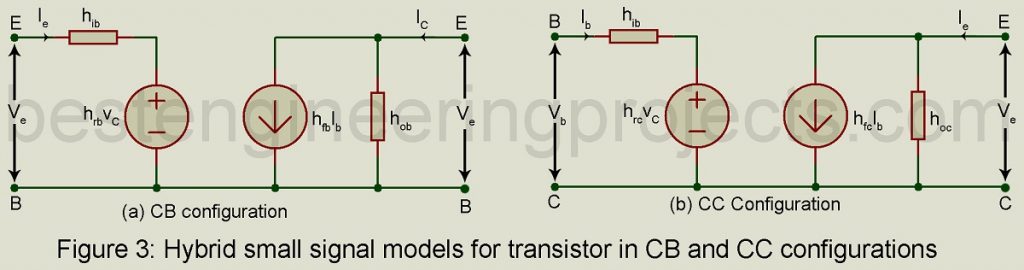
Figure 3 gives the h-parameter models for the transistor in CB and CC configurations. It may be noted that in CC configuration of figure 3(b), B and C are the input terminals while E and C are the output terminals.

Equations (5) and (6) are valid for CE model of figure 2. Similar equations using CB and CC h-parameters may be written respectively for CB and CC models.

For each of the three configurations, application of Kirchhoff’s current law (KCL) gives that the sum of current I_b + I_c + I_e = 0.

The models of Figures 2 and 3 are corresponding equations are valid for both NPN and PNP transistors and are independent of the nature of load impedance or the method of biasing.

Graphical Determination of h-parameters

Static input characteristic curves may be used to determine graphically the parameters h_ie and h_re using equations 7(a) and 7(b) respectively. Similarly, static output characteristic curves may be used to determine h_fe and h_oe using Equations 7(c) and 7(d) respectively.

Variation of transistor h-parameters

All the four h-parameters for any transistor configuration, namely CE, CB and CC, vary with variation of collecto0r current I_C and collector junction temperature. Usually I_C = 1mA is taken as the refence collector current. Similarly, collector junction temperature T_j = 25⁰ is taken as the reference temperature.

Value of h-parameters of a Typical Transistor

Table 1 gives the value of h-parameters of a typical transistor for CE, CB and CC configurations.

Table 1 Values of h-parameters of a Typical Transistor
S.N.	Parameter	CE	CB	CC
1.	h_i	1100Ω	22Ω	1100Ω
2.	h_r	2.5×10^-4	3×10^-4	1
3.	h_f	50	-0.98	-51
4.	h₀	$25\mu S$	$0.5\mu S$	$25\mu S$
5.	1/h₀	40 kΩ	2 MΩ	40 kΩ

Conversion Formulas for h-parameters in the three Configurations

Some manufacturers provide only the four CE h-parameters while other provide h_fe, h_ib, h_ob and h_rb. It is, therefore, often necessary to convert from one set of h-parameters in one configuration to another set in another configuration. Table 2 gives the approximate conversion formulas for h-parameters. These formulas give reasonably accurate results and may be used in almost all cases.

Table 2 Approximate Conversion Formulas for h-parameter
$h_{ic} = h_{ie}$	$h_{ib} = \dfrac{h_{ie}}{1+h_{fe}}$
$h_{fc} = (1+ h_{fe})$	$h_{fb} = -\dfrac{h_fe}{1+h_{fe}}$
$h_{rc} = 1$	$h_{rb} = \dfrac{h_{ie}\times h_{oe}}{1+h_{fe}}-h_{re}$
$h_{oc} = h_{oe}$	$h_{ob} = \dfrac{h_{oe}}{1+h_{fe}}$

Table 2 enables us to compute CC and CB h-parameters if CE h-parameters are known. The expression for CE h-parameters in terms of CB h-parameters may be obtained from Table 2 on interchanging the subscripts b and e.

Derivation of h-Parameter model for transistor

Graphical Determination of h-parameters

Variation of transistor h-parameters

Value of h-parameters of a Typical Transistor

Table 1 Values of h-parameters of a Typical Transistor

Conversion Formulas for h-parameters in the three Configurations

Table 2 Approximate Conversion Formulas for h-parameter

Share this:

Leave a Comment Cancel reply