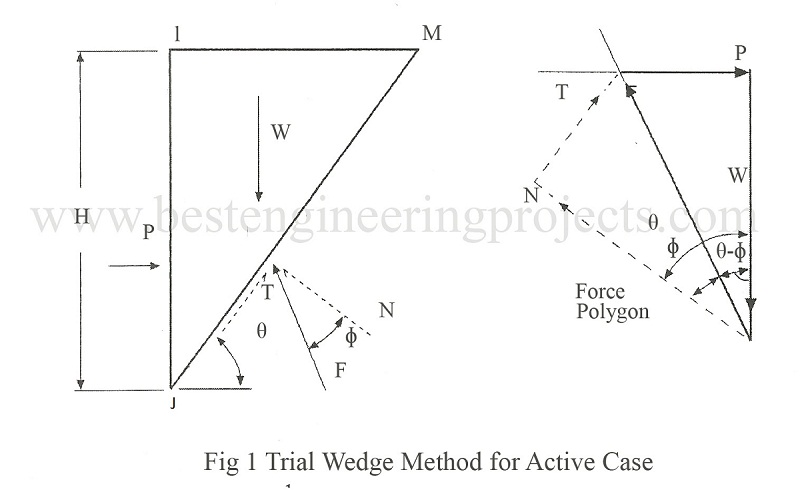
Derivation of Equation by Trial Wedge Method for Active Case

Derivation of Equation by Trial Wedge Method for Active Case: Figure 1 below shows the application of the trial Wedge method to the problem of simple retaining wall without wall friction. A planar failure wedge IJM is considered. There are distributed normal stresses along IJ and JM and distributed shear stress along JM. The resultants of these stresses are carried out in the analysis. The forces acting at the free body IJM are:

let’s start the derivation of equation by trial wedge method

Weight of wedge = $\dfrac{1}{2}\times Area\ IJM \times \gamma$

$= \dfrac{1}{2}\times IM\ IJ \times \gamma$

$= \dfrac{1}{2}\times Hcot\theta \times H \times \gamma$

$= \dfrac{1}{2}\gamma H^2 cot \theta$

P_a = resultant of distributed stresses between soil and wall

N = resultant of normal stresses within soil along assumed plane wall

T = resultant of shear stresses within soil along assumes plane wall

= N tan $\phi$

Considering the equilibrium of the wedge and referring the force polygon we have a sine rule,

$\dfrac{W}{90-(\theta -\phi)} = \dfrac{P_a}{Sin(\theta -\phi)}$

$\dfrac{W}{Cos(\theta -\phi)} = \dfrac{P_a}{Sin(\theta -\phi)}$

or, $P_a = W tan(\theta-\phi)$

or, $P_a = \dfrac{1}{2}\gamma H^2 cot\theta \times tan(\theta-\phi)$ ———-(1)

Now the problem is to find out the maximum value of P which would give the value of earth pressure in active case. This is done by differentiating P with respect to $\theta$ and equating to zero. Then:

$\dfrac{\partial P_a}{\partial \theta} = 0$

$\dfrac{\partial P_a}{\partial \theta} = \dfrac{1}{2}\gamma H^2 [\dfrac{-Tan(\theta -\phi)}{sin^2\theta} + \dfrac{cot \theta}{cos^2(\theta -\phi)}] = 0$